Distances entières

[fahr451]

(une jolie preuve à mon sens):
Soit E une partie infinie du plan eucidien , telle que la distance entre deux points quelconques de E est un entier.Montrer que E est inclus dans une droite.

[Imod]

Bonsoir.

Comme je découvre le sujet avant d'aller me coucher , je peux juste dire que E infini est indispensable ( prendre les sommets d'un triangle rectangle à côtés entiers ) .

Imod

[tize]

Soit A,B et C trois points non alignés de E et M un point de E.
|MA-MB| et |MB-MC| sont des entiers naturels. De plus l'inégalité triangulaire donne et donc et de même .
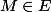Si on appelle et , on peut remarquer avec ce qui a été dit que et aussi . Donc pour tout , il existe des entiers k et p tels que , on peut même dire que qui est une union finie.
Reste à montrer que est fini pour tout k et p.
Je ne me rappelle plus trop mais il me semble que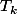 et 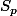représentent des hyperboles dans tous les cas il y a un nombre fini de solutions (4, non ?) sauf si k=0 ou AB et p=0 ou BC, dans ces cas là, on a des droites il me semble...

[fahr451]

absolument.
le cas de dégénérescence pour l hyperbole ( cas d égalité ds l inégalité triangulaire )avec cette définition bifocale est la droite AB privée du segment ("ouvert")AB k =AB . Il y a aussi la médiatrice de [A,B], k = 0
une conique "en général " est définie par 5 points . l'intersection de deux " vraies"hyperboles différentes donne au plus 4 points.
les droites (AB) (AC) étant différentes un point pour l'intersection droite droite.
Et deux points pour le cas intersection droite,hyperbole.