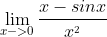
J'ai essayé de remplacer Sin x par Racine de 1-Cos²x mais toujours pas de piste.
Si vous pouviez me donner quelques indices pour y arriver?
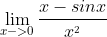
Black Jack a écrit:Bonjour,
Supposons x > 0 et posons g(x) = x - sin(x) + x³
g'(x) = 1 - cos(x) + 3x² forcément > 0 --> g est croissante
g(0) = 0 ---> x - sin(x) + x³ > 0 (pour x > 0)
En divisant par x² > 0, il vient :
(x - sin(x))/x² + x > 0
-x <= (x - sin(x))/x² (1)
h(x) = x - sin(x) - x³
h'(x) = 1 - cos(x) - 3x²
h''(x) = sin(x) - 6x
h'''(x) = cos(x)-6 < 0 --> h'' est décroissante
h''(0) = 0 --> h''(x) < 0 et h' est décroissante
h'(0) = 0 --> h'(x) < 0 et h est décroissante.
h(0) = 0 et donc h(x) < 0
x - sin(x) - x³ < 0
x-sin(x) < x³
et en divisant par x² > 0 les 2 membres -->
(x-sin(x))/x² < x (2)
(1) et (2) donnent :
Pour x > 0, on a -x <= (x - sin(x))/x² < x
Et donc si x--> 0+, on a 0 <= lim(x-->0+) (x - sin(x))/x² < 0
Et donc lim(x-->0+) (x - sin(x))/x² = 0
--------
On procède de manière analogue avec x < 0
...
Non vérifié
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :