salut est-ce que vous pouvez m'aider pour résoudre ces inéquations :
1. 2x < 0
2. -2(4x + 1) + (x-3) > 0
3. (-3x + 9) -2(-4x + 7) < ou = x
4. -1/2 (-2x + 8) + 4/5 (5x -10) > -(x + 2)
5. 5-4x/5 - 3-x/10 < x/2
Inéquations
7 messages
- Page 1 sur 1
Résoudre une inéquation c'est trouver l'ensemble des valeurs de x vérifiant l'inégalité demandée. Ce sont des intervalles de R.
A la fin d'une inéquation du premier degrès tu dois avoir par exemle x0 [/TEX] , on ne change pas le sens de l'inégalité.
d'où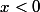 (réel strictement négatif)
(réel strictement négatif)
L'ensemble solution est donc l'ensemble des nombres négatifs
2) Tu procèdes comme suit
a) Tu développes la partie gauche de ton inéquation
b) Tu réduits, c'est à dire tu regroupes les termes en x d'une part et les nombres d'autre part ( ex :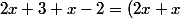+(3-2)=3x+1) )
)
c)Le but est d'arriver à x<..
Je vais te traiter un exemple :
En premier, il faut faire disparaître les nombres (c'est à dire 3) du côté gauche de l'inégalité.
Pour celà on ajoute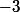 au côté gauche (donc au côté droit)
au côté gauche (donc au côté droit)
d'où) que l'on écrit
que l'on écrit <-3)
ton inéquation devient alors
Comme pour ta première inéquation (la numéro 1), tu multiplies par
 le côté gauche pour obtenir
le côté gauche pour obtenir  .
.
On multiplie , bien sûr, le côté droit (aussi) par
donc tu as [TEX] \frac{1}{2} \times 2 x < -3 \times \frac{1}{2}
donc x<-\frac{3}{2}
Pour la 4 et la 5 avant de résoudre les inégalité, multiplie tes 2 inéquations par 10 (des deux côtés ) pour enlever les fractions.
A la fin d'une inéquation du premier degrès tu dois avoir par exemle x0 [/TEX] , on ne change pas le sens de l'inégalité.
d'où
L'ensemble solution est donc l'ensemble des nombres négatifs
2) Tu procèdes comme suit
a) Tu développes la partie gauche de ton inéquation
b) Tu réduits, c'est à dire tu regroupes les termes en x d'une part et les nombres d'autre part ( ex :
c)Le but est d'arriver à x<..
Je vais te traiter un exemple :
En premier, il faut faire disparaître les nombres (c'est à dire 3) du côté gauche de l'inégalité.
Pour celà on ajoute
d'où
ton inéquation devient alors
Comme pour ta première inéquation (la numéro 1), tu multiplies par
On multiplie , bien sûr, le côté droit (aussi) par
donc tu as [TEX] \frac{1}{2} \times 2 x < -3 \times \frac{1}{2}
donc x<-\frac{3}{2}
Pour la 4 et la 5 avant de résoudre les inégalité, multiplie tes 2 inéquations par 10 (des deux côtés ) pour enlever les fractions.
Résoudre une inéquation c'est trouver l'ensemble des valeurs de x vérifiant l'inégalité demandée. Ce sont des intervalles de R.
A la fin d'une inéquation du premier degrès tu dois avoir par exemle x0 [/TEX] , on ne change pas le sens de l'inégalité.
d'où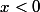 (réel strictement négatif)
(réel strictement négatif)
L'ensemble solution est donc l'ensemble des nombres négatifs
2) Tu procèdes comme suit
a) Tu développes la partie gauche de ton inéquation
b) Tu réduits, c'est à dire tu regroupes les termes en x d'une part et les nombres d'autre part ( ex :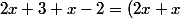+(3-2)=3x+1) )
)
c)Le but est d'arriver à x<..
Je vais te traiter un exemple :
En premier, il faut faire disparaître les nombres (c'est à dire 3) du côté gauche de l'inégalité.
Pour celà on ajoute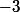 au côté gauche (donc au côté droit)
au côté gauche (donc au côté droit)
d'où<-3)
ton inéquation devient alors
Comme pour ta première inéquation (la numéro 1), tu multiplies par
 le côté gauche pour obtenir
le côté gauche pour obtenir  .
.
On multiplie , bien sûr, le côté droit (aussi) par
donc tu as
donc
Pour la 4 et la 5 avant de résoudre les inégalités, multiplie tes 2 inéquations par 10 (des deux côtés ) pour enlever les fractions.
A la fin d'une inéquation du premier degrès tu dois avoir par exemle x0 [/TEX] , on ne change pas le sens de l'inégalité.
d'où
L'ensemble solution est donc l'ensemble des nombres négatifs
2) Tu procèdes comme suit
a) Tu développes la partie gauche de ton inéquation
b) Tu réduits, c'est à dire tu regroupes les termes en x d'une part et les nombres d'autre part ( ex :
c)Le but est d'arriver à x<..
Je vais te traiter un exemple :
En premier, il faut faire disparaître les nombres (c'est à dire 3) du côté gauche de l'inégalité.
Pour celà on ajoute
d'où
ton inéquation devient alors
Comme pour ta première inéquation (la numéro 1), tu multiplies par
On multiplie , bien sûr, le côté droit (aussi) par
donc tu as
donc
Pour la 4 et la 5 avant de résoudre les inégalités, multiplie tes 2 inéquations par 10 (des deux côtés ) pour enlever les fractions.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
