Exercice f ◦ g et g ◦ f

[Mardov]

Bonjour, je n'ai pas trop de notion sur les fonctions composées.

Merci d'avance pour votre aide. Je dois surtout faire le b)

1. Soient f : N → N et g : N → N les applications definies par
f(n) = 2n

et g(n) = n/2 si n pair
(n − 1)/2 sinon.

(a) Etudier l’injectivite, la surjectivite et la bijectivite de f et g.

(b) Determiner f ◦ g et g ◦ f.

[Mateo_13]

Bonjour Mardov,

donc à , tu appliques d'abord la fonction et ensuite la fonction .

Pour l'autre, c'est dans l'ordre inverse.

Cordialement,

[mathelot]

Bonsoir,
Demontre que:
A) f est injective
B) f n'est pas surjective
C) g n'est pas injective
D) g est surjective

E) si n est pair (on pourra poser n=2k)
(f o g) (n) =n
Sinon
(f o g) (n) =n-1
F)
Si n est pair:
(g o f) (n) =n
sinon
(g o f)(n) =n

Remarque : g est inverse à gauche de f

[Mardov]

Bonsoir, merci pour vos réponses

Donc je dois faire dans les 2 cas de figures ? n pair et n impair ?

[Mardov]

Bonjour, j'en suis donc à :

Si n pair f(g(n)) = 2 (g(x)) = 2 (n/2)

Sinon f(g(n)) = 2 (g(x)) = 2 ( n-1 /2)

et Si n pair g(f(n)) = 2n / 2

Sinon g(f(n)) = (2n-1) / 2

Pouvez vous me corriger ou m'aider si je me trompe. Merci beaucoup pour votre aide. Je dois rendre cet exercice demain

[mathelot]

Bonsoir, merci pour vos réponses

Donc je dois faire dans les 2 cas de figures ? n pair et n impair ?

Oui.
Pour n pair, poser n=2k et pour n impair, poser n=2k+1

[vam]

Bonjour
pourquoi postes-tu ici alors que tu as eu des réponses ailleurs ?

[mathelot]

Bonjour, j'en suis donc à :

Si n pair f(g(n)) = 2 (g(n)) = 2 (n/2)=n

Sinon f(g(n)) = 2 (g(x)) = 2 ( n-1) /2)=n-1

pour tout n g(f(n)) = 2n / 2=n

[mathelot]

on a:
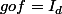application Identique, pour tout entier n,

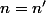
f admet un inverse à gauche g; f est injective et g est surjective.

z=g(f(z)) g est donc surjective puisque tout z est une image par g

f est injective : soient n et n' deux entiers

on compose par g: