Récurrence forte sup
16 messages
- Page 1 sur 1
Récurrence forte sup
Bonsoir je sollicite votre aide pour la qst suivante:
Montrer par récurrence forte que:
(Pour tout n de N*) ( il existe (p,q) de N²) :
n= (2 à la puissance p ) (2q+1)
MERCI!
Montrer par récurrence forte que:
(Pour tout n de N*) ( il existe (p,q) de N²) :
n= (2 à la puissance p ) (2q+1)
MERCI!
Re: Récurrence forte sup
Bonsoir,
Utiliser la récurrence pour ça me semble une drôle d'idée. M'enfin ....
Ou bien n est impair : c'est tout bon.
Ou bien n est pair, et alors n/2 ...
Utiliser la récurrence pour ça me semble une drôle d'idée. M'enfin ....
Ou bien n est impair : c'est tout bon.
Ou bien n est pair, et alors n/2 ...
Re: Récurrence forte sup
Mais monsieur je ne vois pas où vous faites intervenir le principe de récurrence ( on a précisé dans l exercice qu il faudrait montrer la proposition avec une récurrence forte)
Re: Récurrence forte sup
Dans les points de suspension, bien entendu.
(Hypothèse de récurrence : c'est vrai pour tout entier >0 et <n)
(Hypothèse de récurrence : c'est vrai pour tout entier >0 et <n)
Re: Récurrence forte sup
Oui c'est bien ça Monsieur mais c'est à cette étape là que je me bloque, je ne sais pas comment l hypothèse de récurrence va montrer que c'est aussi valable pou (n+1). Pouvez vous m'aider à le faire? MERCI !
Re: Récurrence forte sup
Ici, l'hérédité pour la "récurrence forte" qu'on peut utiliser pour montrer ) pour tout
pour tout 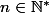 est :
est :
"Si) pour tout
pour tout 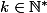 tel que
tel que 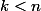 alors
alors ) "
"
(Sous cette forme, on n'a même pas besoin d'initialisation).
"Si
(Sous cette forme, on n'a même pas besoin d'initialisation).
Re: Récurrence forte sup
Bonsoir à tous et en particulier à toi GaBuZoMeu
Pourquoi n'a t-on pas besoin d'initialisation ?
Pourquoi n'a t-on pas besoin d'initialisation ?
Re: Récurrence forte sup
Comme cas particulier de
"Si) pour tout
pour tout 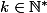 tel que
tel que 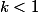 alors
alors ) "
"
La prémisse de cette implication est trivialement vérifiée, n'est-ce pas ?
Je sais parfaitement que cette affirmation "pas besoin d'initialisation" perturbe (je l'ai expérimenté en prépa agreg). Je l'ai mise exprès pour provoquer des réactions.
tu asGaBuZoMeu a écrit:"Sipour tout
tel que
alors
"
"Si
La prémisse de cette implication est trivialement vérifiée, n'est-ce pas ?
Je sais parfaitement que cette affirmation "pas besoin d'initialisation" perturbe (je l'ai expérimenté en prépa agreg). Je l'ai mise exprès pour provoquer des réactions.
Re: Récurrence forte sup
Merci à toi mais alors pour P(n) <=> n=n+1 , on obtient :
)\Rightarrow 1=2)
Le vrai n'implicant pas le faux , on ne peut utiliser ta forme que si on sait ou si on a démontré P(1) , ce qui revient à faire une initialisation en amont de ta présentation .
Le vrai n'implicant pas le faux , on ne peut utiliser ta forme que si on sait ou si on a démontré P(1) , ce qui revient à faire une initialisation en amont de ta présentation .
Re: Récurrence forte sup
Si tu veux montrer ) il suffit de montrer
il suffit de montrer )\right)\Rightarrow P(n)\right))
Si tu as démontré ça, pas besoin d'initialisation. Reste bien sûr à démontrer ça.
Dans l'exercice du questionneur, on le démontre en raisonnant par disjonction des cas : ou bien est impair et c'est fini, ou bien
est impair et c'est fini, ou bien  est pair et on considère
est pair et on considère 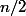 ... tu vois comment conclure.
... tu vois comment conclure.
Je le répète : aucune initialisation n'a été maltraitée dans le tournage de cette séquence.
Si tu as démontré ça, pas besoin d'initialisation. Reste bien sûr à démontrer ça.
Dans l'exercice du questionneur, on le démontre en raisonnant par disjonction des cas : ou bien
Je le répète : aucune initialisation n'a été maltraitée dans le tournage de cette séquence.
Re: Récurrence forte sup
Bonjour et merci
A cause de toi , je me retrouves dans l'enfer des math .
Je vais réflechir à ton explication et te répondre .
A cause de toi , je me retrouves dans l'enfer des math .
Je vais réflechir à ton explication et te répondre .
Re: Récurrence forte sup
Je reste sur ma position tout en me raliant à la tienne:
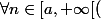
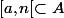
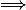
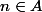 )
)
est bien une caractérisation de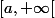 sans initialisation .
sans initialisation .
On peut donc caractériser les intervalles de utilisés dans les récurrences sans initiialisation. Encore faut il démontrer cela , en particulier que a appartient à A .
utilisés dans les récurrences sans initiialisation. Encore faut il démontrer cela , en particulier que a appartient à A .
C 'est indispensable pour que l'implication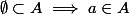 soit vraie .
soit vraie .
Ta présentation de la recurrence pourrait donc être qualifiée de "à initialisation implicite" .
est bien une caractérisation de
On peut donc caractériser les intervalles de
C 'est indispensable pour que l'implication
Ta présentation de la recurrence pourrait donc être qualifiée de "à initialisation implicite" .
Re: Récurrence forte sup
Ècoute, je dis simplement que si on a un procédé uniforme en  pour démontrer
pour démontrer
\qquad\forall n \in \N^*\ \left(\left(\forall q\in \N^* \ (q<n\Rightarrow P(q))\right)\Rightarrow P(n)\right))
alors il n'y a pas besoin de se préoccuper d'initialisation.
Je peux te raconter la démonstration où le fait qu'il n'y a pas besoin d'initialisation choquait certains agrégatifs : il s'agit de montrer
 :) pour tout espace vectoriel de dimension
pour tout espace vectoriel de dimension  et toute famille (finie ou infinie) d'endomorphismes diagonalisables de cet espace vectoriel qui commutent entre eux, il existe une base de diagonalisation commune.
et toute famille (finie ou infinie) d'endomorphismes diagonalisables de cet espace vectoriel qui commutent entre eux, il existe une base de diagonalisation commune.
Démonstration de) sous l'hypothèse
sous l'hypothèse )) : si tous les endomorphismes de la famille sont des homothéties, c'est gagné, n'importe quelle base fait l'affaire. Sinon, au moins un des endomorphismes n'est pas une homothétie, et on applique l'hypothèse aux sous-espaces propres de cet endomorphismes qui sont tous de dimension
: si tous les endomorphismes de la famille sont des homothéties, c'est gagné, n'importe quelle base fait l'affaire. Sinon, au moins un des endomorphismes n'est pas une homothétie, et on applique l'hypothèse aux sous-espaces propres de cet endomorphismes qui sont tous de dimension 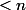 et stables par tous les endomorphismes de la famille. On recolle ensuite les bases de diagonalisation communes de chaque sous-espace propre.
et stables par tous les endomorphismes de la famille. On recolle ensuite les bases de diagonalisation communes de chaque sous-espace propre.
Fin de la démonstration, sans initialisation.
alors il n'y a pas besoin de se préoccuper d'initialisation.
Je peux te raconter la démonstration où le fait qu'il n'y a pas besoin d'initialisation choquait certains agrégatifs : il s'agit de montrer
Démonstration de
Fin de la démonstration, sans initialisation.
Re: Récurrence forte sup
Merci pour ton aide et pour nous avoir fait découvrir sur ce forum cette formulation de la récurrence .
Je ne recommanderais pas à des étudiants de la pratiquer en concours car je suis sûr que certains profs ne la connaissent pas . C'est mon cas , j'ai 67 ans et je ne l'ai jamais rencontrée .
Je ne recommanderais pas à des étudiants de la pratiquer en concours car je suis sûr que certains profs ne la connaissent pas . C'est mon cas , j'ai 67 ans et je ne l'ai jamais rencontrée .
Re: Récurrence forte sup
Bah, ce n'est qu'une version du fait que 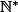 est bien ordonné.
est bien ordonné.
Si l'ensemble des entiers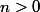 tels que
tels que ) est non vide, alors le plus petit d'entre eux fournit un contre-exemple à l'énoncé (*) plus haut.
est non vide, alors le plus petit d'entre eux fournit un contre-exemple à l'énoncé (*) plus haut.
Si l'ensemble des entiers
Re: Récurrence forte sup
Merci GaBuZoMeu (génial même si pour vous c'est évident moi ça m'a fait un truc)
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
