Calcul intégral
16 messages
- Page 1 sur 1
Calcul intégral
Bonjour tout le monde et merci d’avance pour ce qui vont le lire.
Ça fait quelque heure que j’essaie de faire un calcul intégral qui est :
\int_{0}^{1}{ln(1+\sqrt{x^2 +1})dx}
Par une intégration par partie j’ai trouvé :
ln(1+\sqrt{2}) - \int_{0}^{1}{x^2/(x^2 +1 + \sqrt{x^2 +1})dx}
A partir de là j’ai essayé beaucoup de chose ( changement de variable avec u = \sqrt{x^2 +1} ou encore u = x^2 ) enfin en somme je sens que je suis pas loin, c’est peut une illusion de croire ça possible, mais argsinh(x) a pour dériver 1/\sqrt{x^2 +1} je voulais prendre ça comme nouveau point de départ, mais je reste quand même bloqué si je fais une autre intégration par partie! Merci d’avoir lu le message malgré la mauvaise qualité d’expression et merci pour tout indices que vous pouvez donner!
Ça fait quelque heure que j’essaie de faire un calcul intégral qui est :
\int_{0}^{1}{ln(1+\sqrt{x^2 +1})dx}
Par une intégration par partie j’ai trouvé :
ln(1+\sqrt{2}) - \int_{0}^{1}{x^2/(x^2 +1 + \sqrt{x^2 +1})dx}
A partir de là j’ai essayé beaucoup de chose ( changement de variable avec u = \sqrt{x^2 +1} ou encore u = x^2 ) enfin en somme je sens que je suis pas loin, c’est peut une illusion de croire ça possible, mais argsinh(x) a pour dériver 1/\sqrt{x^2 +1} je voulais prendre ça comme nouveau point de départ, mais je reste quand même bloqué si je fais une autre intégration par partie! Merci d’avoir lu le message malgré la mauvaise qualité d’expression et merci pour tout indices que vous pouvez donner!
Re: Calcul intégral
Bonjour,
je te laisse régler le problème des bornes et ajouter le signe -
en faisant une IPP, tu dois intégrer
\sqrt{x^2+1}}dx<br />\end {aligned})
pose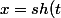) ; en remplaçant tu obtiendras finalement
; en remplaçant tu obtiendras finalement
-1] dt<br />\end {aligned})
sauf erreur de ma part
je te laisse régler le problème des bornes et ajouter le signe -
en faisant une IPP, tu dois intégrer
pose
sauf erreur de ma part
Re: Calcul intégral
Après vérification, ce changement de variable est peut être pas le bon, puisque après plusieurs essaie, c’est loin de la réponse que j’ai trouvé en analysant la représentation graphique de la fonction. Merci quand même de m’avoir donner l’idée de changer de variable avec une fonction hyperbolique.
Re: Calcul intégral
J’ai trouvé 0,75 ( c’est une lecture graphique à vue d’œil donc pas très précis) mais je suis sûr que ça tourne autour de ça
Re: Calcul intégral
Excusez moi, erreur de jugement ( désolé de vous avoir fais perdre du temps sur une inattention)
Re: Calcul intégral
pas très sympa de demander une réponse sur un autre forum 
ça fait perdre du temps au bénévole qui te répond!
ça fait perdre du temps au bénévole qui te répond!
Re: Calcul intégral
On m’a cramé, j’essayais pas d’être sournois mais d’avoir le plus d’avis sur le problème, désolé si ça vous dérange!
Re: Calcul intégral
tu as de la chance car sur certains forums les modérateurs bloquent l'accès en cas de multisite
maintenant, je ne devrais pas, mais si tu as d'autres questions je veux bien te répondre
maintenant, je ne devrais pas, mais si tu as d'autres questions je veux bien te répondre
Re: Calcul intégral
Ah oui carrément, bon c’est pas juste une petite bêtise, je ne le referais plus soyez en certain!
Puisque c’est ma première année de prépa, je vais commencer le vendredi prochain, l’exercice proposé demande énormément de hors programme mais puisque avoir de la culture n’est pas interdite, ces méthodes ne sont pas étrangères, j’aurais juste aimé savoir l’intuition qui vous a mené à ce changement de variable et également, qu’est ce que vous pensez de l’exos ?
Puisque c’est ma première année de prépa, je vais commencer le vendredi prochain, l’exercice proposé demande énormément de hors programme mais puisque avoir de la culture n’est pas interdite, ces méthodes ne sont pas étrangères, j’aurais juste aimé savoir l’intuition qui vous a mené à ce changement de variable et également, qu’est ce que vous pensez de l’exos ?
Re: Calcul intégral
en général quand tu as un radical avec un carré + une valeur le sh marche bien mais souvent on peut aussi utiliser le changement x=tan(t)
On travaille aussi par expérience
Avec le temps on attrappe le flair
Quant à l'exo il fait réfléchir!
Tu peux toujours t'entraîner en résolvant d'autres exercices
On travaille aussi par expérience
Avec le temps on attrappe le flair
Quant à l'exo il fait réfléchir!
Tu peux toujours t'entraîner en résolvant d'autres exercices
Modifié en dernier par Pisigma le 29 Aoû 2021, 15:26, modifié 1 fois.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
