Bien le bonjour cher lecteur,
Soient les points dans le plan :
A(-2, -4) - B(6, 3) - D(-7, -1)
On par conséquent le vecteur AB de coordonnées (8, 7)
Je veux trouver le point C pour lequel les vecteurs AB et DC sont colinéaires.
J'ai procédé par deux manières.
La première par le produit vectoriel.
vec(AB) * vec(DC) = AB*DC (puisque cos(0) = 1)
J'ai donné une coordonnée d'abysses de 1 à C pour faciliter le calcul sinon on aura une équation à deux inconnus. Et une norme de 6 pour DC puisque ce n'est pas important puisque DC serait un vecteur directeur d'une droite étant parallèle à l'autre droite à vecteur directeur AB.
on a donc vecDC(8, Yc+1) et vecAB(8,7)
en élaborant l'expression par analytique: 8² + (Yc +1) *7 = 6 * 113^(0.5)
En solvant pour Yc j'ai trouvé Yc = -1.031 donc C(1, -1.031) en calculant la norme de DC j'ai trouvé 8 qui n'est pas égal à 6. Et DC d'après ce que j'ai dessiné coupe AB dans un point qui ne doit pas être le cas.
Est-ce-que la colinéarité entre deux vecteurs, veut dire que leur droite respectives n' ont point le même coefficient directeur? ça n'a pas été le cas puisque il se coupent d'ailleurs.
J'ai procédé par une autre manière, vecAB et vecDC seront colinéaire si vecDC/vecAB = k
J'ai toujours mis Xc = 1 pour calculer Yc
vecDC = vecAB*k équivaut à (8, Yc+1) = k (8,7)
k ne peut être que 1 pour que 8 = 8
donc Yc + 1 = 7
Yc = 6
Donc DC(8, 7), qui cette fois confondu avec vec(AB)
Il y aura donc une infinité de points C?
Une colinéarité ne stipule donc pas la même coefficient dir. des respectives droites?
J'ai l'impression que je zappe quelque chose ici..
Si j'ai commis une grosse bêtise merci de me le signaler, je rafraîchis ma mémoire en géométrie de plan, avant de passer à celle de l'espace.
Une question, y a t-il une relation entre la géométrie de plan et les fonctions d'une seule variable, et la géométrie de l'espace et une fonction à deux variables par exemple?
Bien à vous
Géométrie de plan et d'espace
3 messages
- Page 1 sur 1
Re: Géométrie de plan et d'espace
Bonjour,
Voie la plus directe.
2 vecteurs (a ; b) et (c ; d) sont colinéaires ssi a/c = b/d
************
C(X;Y)
D(-7;-1)
vect(DC) = (-7-X;-1-Y)
vect(AB) = (8 ; 7)
Les vecteurs AB et DC sont colinéaires ssi (-7-X)/8 = (-1-Y)/7
Tu exprimes X en fonction de Y ou bien tu exprimes Y en fonction de X
On arrive par exemple (essaie) à X = (8Y-41)/7
---> C((8Y-41)/7 ; Y) avec Y un réel quelconque.
****
exemple numérique : si on choisit Y = 1 --> C(-33/7 ; 1)
vect(DC) = (-7 + 33/7 ; -1-1) = (-16/7 ; -2)
On peut, bien entendu choisir Y = n'importe quel réel.

Voie la plus directe.
2 vecteurs (a ; b) et (c ; d) sont colinéaires ssi a/c = b/d
************
C(X;Y)
D(-7;-1)
vect(DC) = (-7-X;-1-Y)
vect(AB) = (8 ; 7)
Les vecteurs AB et DC sont colinéaires ssi (-7-X)/8 = (-1-Y)/7
Tu exprimes X en fonction de Y ou bien tu exprimes Y en fonction de X
On arrive par exemple (essaie) à X = (8Y-41)/7
---> C((8Y-41)/7 ; Y) avec Y un réel quelconque.
****
exemple numérique : si on choisit Y = 1 --> C(-33/7 ; 1)
vect(DC) = (-7 + 33/7 ; -1-1) = (-16/7 ; -2)
On peut, bien entendu choisir Y = n'importe quel réel.
 Re: Géométrie de plan et d'espace
Re: Géométrie de plan et d'espace
Bonjour,
Je ne veux rien rajouter à ce qu'a dit Black Jack mais revenir sur votre première méthode.
Elle peut être utilisée mais si on a vraiment du temps et envie de se compliquer la vie.
Comme c'est mon cas je reprends par le menu..
je reprends par le menu..
Il s'agit du produit scalaire.
Non c'est :
car l'angle est nul ou plat donc le cosinus vaut +1 ou -1.
ce qui est équivalent à^2 = AB^2 \times CD^2)
Si C a pour coordonnées (1;y)
On obtient l'équation
)^2=113\times(64+(y+1)^2))
ou encore (cette suite d'équations équivalentes entre elles)
^2=113(y^2+2y+65))


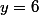
Voilà on trouve le bon résultat mais après pas mal de calculs fastidieux... (à éviter donc)
Un dernier mot sur le coefficient directeur.
En effet deux droites parallèles (ici (AB) et (CD)) ont même coefficient directeur, mais à condition d'en avoir un !!
En effet les droites parallèles à l'axe des ordonnées n'ont pas de coefficient directeur (équation x=k), donc il faut commencer par dire que (AB) n'est pas dans ce cas de figure avant d'utiliser le coefficient directeur.
Toutefois cette méthode est rapide également et fournit bien sûr y=6.
Je ne veux rien rajouter à ce qu'a dit Black Jack mais revenir sur votre première méthode.
Elle peut être utilisée mais si on a vraiment du temps et envie de se compliquer la vie.
Comme c'est mon cas
 je reprends par le menu..
je reprends par le menu..Serendipity19 a écrit:La première par le produit vectoriel.
Il s'agit du produit scalaire.
vec(AB) * vec(DC) = AB*DC (puisque cos(0) = 1)
Non c'est :
car l'angle est nul ou plat donc le cosinus vaut +1 ou -1.
ce qui est équivalent à
Si C a pour coordonnées (1;y)
On obtient l'équation
ou encore (cette suite d'équations équivalentes entre elles)
Voilà on trouve le bon résultat mais après pas mal de calculs fastidieux... (à éviter donc)
Un dernier mot sur le coefficient directeur.
En effet deux droites parallèles (ici (AB) et (CD)) ont même coefficient directeur, mais à condition d'en avoir un !!
En effet les droites parallèles à l'axe des ordonnées n'ont pas de coefficient directeur (équation x=k), donc il faut commencer par dire que (AB) n'est pas dans ce cas de figure avant d'utiliser le coefficient directeur.
Toutefois cette méthode est rapide également et fournit bien sûr y=6.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
