Aide exercice entre terminale et prépa

[Kazu]

Bonjour,
J'ai du mal avec l'exercice ci-dessous. Pour la question une j'ai essayé d'utiliser le théorème des valeurs intermédiaires sans succès, j'ai finalement remarqué que la fonction f était croissante de [0;1] puis décroissante [1;infini[ et que dcp pour x appartenant à R+ il n'y a qu'un unique alpha pour lequel f'(alpha)=0. Cependant je ne pense pas que la justification soit suffisante.
Exercice 20 : Soit f : R+ → R définie par f(x) = x/(e^x+1) .
1. Montrer qu’il existe un unique α ∈ R+ tel que f'(α) = 0. On ne cherchera pas à expliciter α.
2. Montrer que f(α) = α − 1.
3. Donner le tableau de variations de f.

[lyceen95]

J'ai des doutes.
Tu dis que tu as trouvé que f est croissante sur 0,1 puis décroissante.
Donc le point serait le maximum de cette fonction, et serait égal à 0.
Donc serait égal à 1.

Et l'énoncé dit : ne vous embétez pas à calculer (sous-entendu, c'est trop compliqué)
Et l'énoncé dit aussi que serait égal à ... ce qui n'est pas le cas si on dit que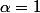

Vérifie tes calculs.