Bonjour,
L'équation du plan du parallélogramme est : x + 5y - 7z + 11 = 0
Les vecteurs normaux au plan sont de la forme v(k ; 5k ; -7k) avec k un réel quelconque différent de 0.
Avec k = -1 ... on retrouve le vecteur que tu as donné.
Mais (comme on te l'a déjà dit), il y en a une infinité d'autres (avec des valeurs de k différentes (sauf 0))
avec k = -2 ou k = -0,1 ou k = 1, on trouve les vecteurs w, u et -v proposé par lycéen95.
*******
Comme lyceen 95 te l'a expliqué, il n'y a pas un seul vecteur normal au plan, il y en une infinité.
Et tous ces vecteurs peuvent évidemment avoir des normes différentes
avec v(1 ; 5 ; -7), on a |v| =
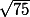
mais on a w(-2,-10,14) et |w| =
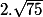
et aussi u(-0.1, -0.5, 0.7) et |u| =
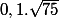
... et tous ces vecteurs (v , w, u ...) sont des vecteurs normaux au plan du parallélogramme.
Peut-on alors dire que la norme de tous les vecteurs normaux au plan du parallélogramme est la même ? et donc ...
************
L'analogie avec les feuilles d'un chêne est parlante.
Si on te demande de prendre une feuille sur un chêne ... tu as le choix entre de multiple feuilles.
Elles ont toutes une caractéristique commune (qui est d'appartenir au chêne)
Et cependant, elles sont toutes différentes (pas la même forme, pas le même poids, pas la même taille ...).
C'est pareil dans ton exercice.
On te demande de calculer UN vecteur normal au plan ... tu as le choix entre de multiples vecteurs (il y en a même une infinité de possibles).
Ils ont tous une caractéristique commune (qui est d'être normal au plan du parallélogramme)
Et cependant, ils sont tous différents (pas la même norme (sauf avec leur vecteur opposé ... (comme v et -v)).
OK ?

.



