Vecteur

par **max38430** » 12 Déc 2006, 09:12

bonjour j'ai un exercice et je suis vraiment coincé.
le voici
ABCD est un parallèlogramme.
M et N sont les points tels que
vecteur AM= 2/3 du vecteur AB
et vecteur CN= 2/3 du vecteur CD

1/ Démontrer que BMDN est un parallèlogramme.
2/ La droite (AC) coupe (DM) en E et (BN) en F.
Déterminer les réels k,k',h tels que
vecteur AE = k*vecteur AC
"" " EF = k'* " " AC
" AF = h* " " AC

Si vous pourriez me donner un petit coup de main se serait sympa
merci

par **maturin** » 12 Déc 2006, 10:50

voici plusieurs définitons/caractéristiques du parallélogramme:
ABCD est un parallélogramme ssi
(1) ses côtés sont parallèles 2 à 2
(2) deux de ses côtés sont parallèles et ont meme longueurs (AB//CD et AB=CD)
(3)

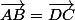
normalement tu dois au moins connaitre (1) et (2)
le (3) découle automatiquement du 2 (avec une orientation en plus).

Donc si tu pars de (3) (je n'écris plus les flèches des vecteurs mais ça en est)
ABCD parallélogramme donc AB=DC
AM=2/3AB => BM=1/3 BA
CN=2/3CD => DN=1/3DC
donc BM=1/3AB=1/3DC=DN donc BMDN parallélogramme.

par **maturin** » 12 Déc 2006, 11:10

pour la deuxième question tu appliques thales dans ABF
AM=2/3AB donc AE=2/3AF
hors AF=AC+CF
par symétrie CF=EA=-AE

donc AE=2/3(AC-AE)
donc 5/3AE=2/3(AC)
AE=2/5AC

par symétrie CF=2/5CA donc AF=3/5AC

par **max38430** » 12 Déc 2006, 11:23

maturin a écrit:pour la deuxième question tu appliques thales dans ABF
AM=2/3AB donc AE=2/3AF
hors AF=AC+CF
par symétrie CF=EA=-AE

donc AE=2/3(AC-AE)
donc 5/3AE=2/3(AC)
AE=2/5AC

par symétrie CF=2/5CA donc AF=3/5AC

salu merci bocou mai enfaite je conpren pa tro les calcul tu pourais pa me les detaill en entier parce tu c'est je uis longue a comprendre mdr
merci

par **maturin** » 12 Déc 2006, 11:34

ben si t'as fait un dessin suffisamment clair.
tu regardes le triangle ABF et le segment ME

comme MBND parllélogramme tu as [ME] parallèle à [BF] tu peux donc appliquer le théroème de Thalès.
tu as AE/AF=ME/BF=AM/AB en longueur.
La version avec vecteur est à peu près la même sauf que tu dois faire un effort pour orienter, et tu dois plus faire de division mais dire AE=xAF, AM=xAB, ME=xBF.

Après j'ai dit que ta figure est symértique par rapport au centre de ton aprallélogramme. A est le symétrique de C, E le symétrique de F...
Donc tu en déduis AE=-CF
et AF=AC+CF d'après al relation de Chasles
donc AF=AC-AE

Voilà je peux pas être bcp plus précis, essaye de faire une figure propre et de suivre mes explcations pas à pas.

par **yvelines78** » 12 Déc 2006, 11:34

bonjour,

pour la 2, je ne sais pas si il y a une solution vectorielle, mais on peut utiliser Thalès
(AC) et (MD) sécantes en E
(AM)//(DC)
A, E et C d'une part et D, E, et M d'autre part alignés dans cet ordre
AE/EC=EM/ED=AM/CD
AE/EC=(2AB/3)/AB=2/3
3AE=2EC
avec AE+EC=AC
3AE=2(AC-AE)
3AE=2AC-2AE
5AE=2AC
AE=2AC/5, donc vecAE=2/5*vecAC

de même on trouve que FC/FA=2/3 et que FA=3/5*AC ou vecFA=3/5*vecAC

puis EF=FA-AE=(3/5*AC)-(2/5*AC)=1/5*AC, donc vecEF=1/5*vecAC

Vecteur

vecteur

Qui est en ligne