Démonstration difficile

[abc]

Soit m et n des entiers supérieurs à zéro, je veux montrer que l'expression
(m^4)+24(m^3)(n^1)+144(m^2)(n^2)+288(m^1)(n^3)
ne peut être un carré pour tout m et n.
J'ai essayé de faire une démonstration avec la récurrence , la descente infinie et par l'absurde et rien ne fonctionne. Quelqu'un peut-il m'aider dans cette démonstration? Merci à l'avance.

[azf]

Bonjour

Soit m et n des entiers supérieurs à zéro, je veux montrer que l'expression
(m^4)+24(m^3)(n^1)+144(m^2)(n^2)+288(m^1)(n^3)
ne peut être un carré pour tout m et n.

Obiter dictum n^1=n

pour le reste si on prend m=n=1 l'expression n'est pas un carré

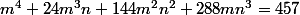pour m=n=1

457 n'est pas un carré

[catamat]

Bonjour

Je suppose que abc souhaite démontrer que quels que soient les entiers, non nuls, m et n, il n'existe pas d'entier k tel que l'expression donnée soit égale à k².

Je n'ai pas trouvé pour le moment mais l'expression peut s'écrire aussi :

[lyceen95]

Ou encore, sauf erreur :

Pas forcément plus simple, mais comme la formule ressemblait beaucoup à ...

[abc]

Merci catamat, vous avez effectivement compris que la démonstration doit se faire pour toutes les valeurs entières de m et n plus grandes que zéro. J'avais observé aussi la possibilité de cette réécriture de l'expression mais ça ne facilite rien pour la démonstration.