Topologie: Homéomorphisme

[Xavier63]

J'ai du mal à m'imaginer le graphe de l'application identité f de (IR, d_dis) dans (IR, d) où (d : étant la distance usuelle, d_dis : la distance discrète)
____________________
Homéomorphisme
l'application identité f de (IR,d) dans (IR, d) est un homéomorphisme (d étant la distance usuelle)
Je comprends, dans ce cas que le graphe est la première bissectrice, donc elle est continue et on a une bijection, et f^-1 est continue
____________________________________________________________________
exemple d'application qui n'est pas un Homéomorphisme :
Il est dit que l'application identité f de (IR, d_dis) dans (IR, d) est continue, mais f^-1 n'est pas continue (d_dis étant la distance discrète, d: la distance usuelle)
si je ne me trompe pas, l'ensemble de définition de f est {0,1} et non IR, enfin je n'arrive pas à imaginer cette application identité

Merci pour votre aide

[GaBuZoMeu]

Bonjour,

L'application identité est toujours l'application identité, son graphe dans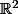 est toujours la première bissectrice.

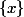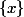Ce qui change c'est la topologie et la topologie ne se voit pas sur le dessin. Pour la topologie discrète, le singleton est un voisinage du réel . On ne peut évidemment pas faire rentrer un intervalle ouvert contenant dans le singleton . C'est ça, le fait que l'application identité 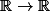n'est pas continue quand on met la topologie ordinaire au départ et la topologie discrète à l'arrivée.

[Xavier63]

Bonjour

Je ne suis pas sûr d'avoir tout compris !

Si j'applique la définition de la continuité :

(qq soit e > 0, il existe a > 0, qq soit x élément de IR) (d(b,x) < a ==> d_dis( f(b) , f(x) ) < e) ne se vérifie pas alors que :
(qq soit e > 0, il existe a > 0, qq soit x élément de IR) (d_dis(b,x) < a ==> d( f(b) , f(x) ) < e ) se vérifie

Je ne vois pas bien

Merci pour l'aide

[Xavier63]

Est-ce bien cela?

[GaBuZoMeu]

On parle de la fonction identité, la fonction définie pas pour tout x de . Peux-tu me dire quel est l'ensemble des 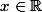tels que la distance discrète de à soit strictement plus petite que 1 ?