Une limite à calculer
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pololapino
- Messages: 3
- Enregistré le: 01 Juil 2021, 10:09
-
 par Pololapino » 01 Juil 2021, 10:21
par Pololapino » 01 Juil 2021, 10:21
Bonjour,
Je dois calculer la limite suivante :
^xln(x)}{x^x-1})
lorsque x tend vers 0
Alors voici ma démarche :
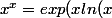)=1+xln(x)+o(xln(x)))
donc

est équivalent à
)
en 0.
Ensuite,
^x = exp(xln(x^x))=exp(xln(1+xln(x)+o(xln(x)))=exp(x^2 ln(x)+o(x^2 ln(x)) = 1+x^2 ln(x)+o(x^2 ln(x)))
Et donc
^x ln(x))
est équivalent à
)
, et le quotient de départ est équivalent à
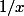
, donc il diverge en 0. Je suis censé trouver que la limite est 1. Pourriez-vous m'aider à trouver mon erreur ?
Merci, bonne journée !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Juil 2021, 10:44
par GaBuZoMeu » 01 Juil 2021, 10:44
Bonjour,
Pas d'erreur, et on peut faire plus simple.
Quand
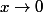
:
^x= x^{x^2}=\exp(x^2\ln(x)))
tend vers 1, donc le numérateur est équivalent à
)
,
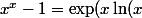)-1)
est équivalent à
)
.
je pense qu'il y a une coquille dans ton énoncé. Tu es sûr que c'est
^x)
et pas
})
?
-
Pololapino
- Messages: 3
- Enregistré le: 01 Juil 2021, 10:09
-
 par Pololapino » 01 Juil 2021, 11:21
par Pololapino » 01 Juil 2021, 11:21
Bonjour, merci pour ta réponse, en fait il n'y a pas de parenthèses dans l'énoncé (mais je n'ai pas réussi à l'écrire sans parenthèses avec l'éditeur d'équations). Comment l'interpréter sans parenthèses ? et dans ce cas y a-t-il une erreur dans le raisonnement ?
Merci !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Juil 2021, 11:26
par GaBuZoMeu » 01 Juil 2021, 11:26
D'accord, c'est que tu as mal interprété l'énoncé. La "règle de priorité" pour les exposants est "du plus haut au plus bas" :

est
})
.
-
Pololapino
- Messages: 3
- Enregistré le: 01 Juil 2021, 10:09
-
 par Pololapino » 01 Juil 2021, 16:47
par Pololapino » 01 Juil 2021, 16:47
Ok merci !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités