Méthode numérique bissection

[Saida1402]

Bonjour ! Voici mon exercice :
Soit :
f(x)= (x^2-9)*(x^3-1)/0.625
1) Faire 5 itérations de la méthode de Bissection sur l’intervalle [0.7 2] :
S=3 et Arrondi.
2)Déterminer le nombre d’itérations nécessaires pour obtenir une précision de 10^(-3)avec la méthode précédente.

Alors, j'ai fait la première question et j'ai trouvé c5= 0.986 et f(c5)= 0.532
Puis, pour la deuxième question, j'ai continué de faire des itérations dans le but de trouver cn avec lequel
f(cn)<10^(-3) mais j'en suis à 10 itérations et on ne dirait même pas que je me rapproche de la réponse...

Je ne sais pas si je me suis trompée quelque part ou si je suis censée faire encore plus d'itérations, mais je n'ai vraiment pas l'impression d'arriver quelque part. Pouvez-vous m'aider s'il vous plait ?

Merci d'avance !

[GaBuZoMeu]

Bonjour,

Ton énoncé est difficilement compréhensible. Pourrais-tu le recopier plus exactement ?

[Saida1402]

Bonjour!

C'est l'énoncé exact de mon professeur, je ne sais pas vraiment comment expliquer plus. Pourriez-vous me dire ce qui n'est pas clair précisément ?

[catamat]

Bonjour

Il semble que ce soit la résolution de f(x)=3 par bissection de l'intervalle [0.7;2]

Comme l'amplitude de l'intervalle est divisé par 2 à chaque itération, à la dixième itération on aura divisé par 2^10 soit 1024 donc l'amplitude sera 0,0012 , le centre de cet intervalle répond donc à la question.

[Saida1402]

Bonsoir,

Désolée je ne m'étais pas rendue ompte que je n'avais pas écrit qu'on cherche la solution de f(x)=0 par méthode de bissection. Et justement, on faisant mes 5 itérations j'en arrive à c5=0.986, ce qui veut dire que je me rapproche de 1 qui est effectivement une solution à l'équation f(x)=0

Seulement je ne trouve pas ensuite le nombre d'itération nécessaire pour avoir une précision de 10^-3

[mathelot]

Bonsoir,
on parle aussi de dichotomie, "tomeo" en grec veut dire "couper" et "dicho" "en deux".
Dichotomie veut dire couper en deux.

Ceci écrit, je trouve que le concepteur de l'exercice aurait pu prendre un nombre transcendant comme racine (par exemple la racine de l'équation f(x)=cos(x)-x=0)

[GaBuZoMeu]

Bonsoir,

Je n'ai toujours pas compris à quoi servait "S=3 et Arrondi" dans ton énoncé;
Pour la précision de 10^(-3), Catamat a pratiquement traité la question pour toi !

[lyceen95]

Dans un de tes messages, tu dis que tu cherches à arriver à ... ou disons plutôt
Mais non, ce n'est pas ça qu'on cherche.
On cherche un intervalle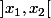 d'amplitude 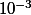, et pour lequel on a l'assurance que la fonction admet un dans cet intervalle.

[Saida1402]

Bonsoir,
Merci de vos réponses !
En fait, mon professeur répond à ce genre de question (celle concernant la précision) d'une toute autre manière (celle que j'ai mentionné du /f(x)/<10^-3), c'est pour cela que je n'avais pas bien compris la réponse de catamat.

J'ai bien compris le concept maintenant grâce à lyceen95, merci encore !!