Pb géométrie et intégration: courbe x^a+y^a= cste

[Abies]

Bonjour,
je suis confronté à un problème d'intégration. En effet je m'intéresse à des courbes definies dans un espace 2D par l'equation en coordonnées cartésiennes:
x^a +y^a=c
avec a et c deux nombre réel positifs et a>=2.

En fait le cas particulier a=2 est un cercle. Le cas a-> infini est un carré.

Je souhaite d'une part calculer la longueur du contour de la courbe = périmètre et d'autre part son aire.
Toutefois, je peine à identifier le changements de variables conduisant à une expression en primitives connues. J'ai d'autre part échoué en passant en coordonnées polaires.

Quelqu'un ici aurait il la réponse ? Merci

[Pisigma]

Bonjour,

tu devrais nous en dire un peu plus.

dans certains cas tu pourrais obtenir des courbes qui ne sont pas fermées

[Abies]

Les courbes qui m'intéressent sont celles correspondant a la transformation d'un cercle de diamètre d en carré de même centre et de côté d.
Initialement la courbe pour a =2 est un cercle, il s'agit de la courbe de depart. Pour simplifier prenons c=1, on a le cercle unité centré en (0,0).
La famille de courbe concernée est alors
x^a+y^a=1 avec a>=2

Je m'intéresse à la famille de courbe qui lorsque a -> infini va tendre vers un carré de sommets (1,1) (1,-1) et donc de centre (0,0).

Donc dans mon cas ces courbes devraient être fermées. Je souhaite évaluer le périmètre et l'aire en envisageant la possibilité d'une formule analytique.

Voilà j'espère que c'est plus clair.

[GaBuZoMeu]

Bonsoir,

Tu ferais mieux d'écrire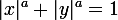 . Tu as un problème de définition de 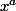quand est négatif et réel, et tu as aussi un sérieux problème avec (demande à GeoGebra de dessiner cette courbe).