Comparaison série intégrale

[Samoth]

Bonjour,

Voici la question sur laquelle je bloque (extrait de mp ccp 2016).
Pour tout entier , on pose .
La question est la suivante : Utiliser un théorème du cours pour justifier simplement que la série converge.

Bien, je pense naturellement au fait que si est définie, continue, positive et décroissante sur tout intervalle de la forme , avec , alors est de même nature que .

Dans la correction, on propose d'appliquer ce résultat à la fonction définie sur par .

Je ne vois cependant comment passer de à , et le lien avec ?

Voyez-vous ce que je manque ?!
Merci !!

[jbreuil]

Bonjour
j'essaierais l'inégalité de la moyenne. l'intégrale est comprise entre 1/n et 1/(n-1).On ote 1/n et on somme.

[Samoth]

Merci jbreuil pour ta réponse.

En utilisant ton idée, j'aboutis à .

Je ne vois toujours pas comment conclure.

[hdci]

Bonjour,
Une façon de traiter : théorème, si deux suites de termes positifs sont équivalentes, alors les séries correspondantes sont équivalentes.
Cherchez donc un terme équivalent au terme indiqué pour lequel on sait que la série est convergente.

Ou sinon : en obtenant le fait que les sommes partielles sont bornées, quel est le signe de chaque terme ; par conséquent que peut-on dire du sens de variation de la somme partielle ; avec les bornes que peut-on en déduire.

Attention toutefois, tant que vous ne savez pas que la série converge, vous n'avez pas le droit d'écrire

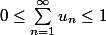
Car le terme entre les deux inégalités est nécessairement un nombre, ledit nombre n'existant pas si la série diverge. si vous n'avez pas la conclusion "la série converge" vous devez écrire

[hdci]

Autre remarque (puisque le titre est "comparaison série intégrale") : faites une figure en traçant la courbe inverse.
A quoi correspond la série des 1/n, géométriquement, par rapport à cette courbe ? Il y a deux façons de le voir, une qui "majore" l'autre qui "minore" l'intégrale de ladite fonction inverse (pensez à une fonction "en escalier", constante sur chaque intervalle [k,k+1[).

[jbreuil]

Bonjour hdci,
L'interprétation géométrique est en effet à signaler, j'aurais dû.
Pour répondre à Samoth, je propose:
Les termes de la série étant positifs la série est croissante et majorée, donc converge.
Me trompé-je?

[hdci]

Oui c'est cela.

[Samoth]

Merci à vous deux pour vos idées et indications !

[jbreuil]

De rien, bonne soirée à tous les deux