Bonjour à tous,
Soit x un réel strictement positif. Soit n un entier sup ou égal à 1.
Comment exprimer l'intégrale sur ]0,1] de [t^(nx) (ln t)^(n-1)][t^x (ln t)]dt en fonction de n, x et l'intégrale sur ]0,1] de [t^(nx)(ln t)^(n-1)]dt ?
Je pense aux IPP sur un sous-intervalle ]epsilon,1] mais je ne trouve pas...
Intégrale
5 messages
- Page 1 sur 1
Re: intégrale
Bonjour,
voici mon calcul , sauf erreur de ma part vos intégrales sont de la forme voici mon calcul :
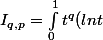^p dt)
IPP :
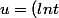^p) soit
soit ^{p-1}t}{t})
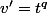 soit
soit 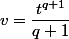
on a donc
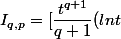^p]_0^1 -\int_0^1 \dfrac{t^{q+1}}{q+1}( lnt)^{p-1}dt =-\dfrac{p}{q+1}I_{q,p-1})
voici mon calcul , sauf erreur de ma part vos intégrales sont de la forme voici mon calcul :
IPP :
on a donc
Re: intégrale
C'est exact (sauf une petite erreur pour u') mais comment ensuite exprimer l'intégrale sur ]0,1] de t^(nx+x) (lnt )^(p-1) dt en fonction de n (sup ou égal à 1), x (strictement sup à 0) et l'intégrale sur ]0,1] de t^(nx) (ln t)^(p-1) dt ?
Re: intégrale
soit :
.................................................................................................................
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
