Rayon de convergence

[moijesuissansE]

Bonjour,
je ne comprends pas ce qu'est un rayon de convergence d'une série entière, après la lecture de cours et de nombreux sites web, cela reste flou et incompréhensible pour moi.
Quelqu'un pourrait m'expliquer svp ?

[mathelot]

Bonsoir, un nombre réel est défini par une coupure. Par exemple est définie par les deux ensembles de rationnels A et B avec
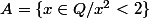et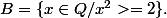
On appelle ça une coupure de Dedekind.

Soit une série entière . Les sont des nombres complexes et z est une variable complexe.
On pose
Une telle série définit une coupure R (donc un réel) avec les ensembles suivants:
et

[moijesuissansE]

Merci beaucoup mais je n'ai pas tout compris... A quoi correspond le rayon de convergence ici ?

[hdci]

Si votre série entière est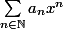
Le rayon de convergence correspond à la borne supérieure des pour lesquels la série est absolument convergente.

Donc pour tout inférieur strictement en valeur absolue à ce rayon, la série converge absolument.
Pour tout supérieur strictement en valeur absolue à ce rayon, la série diverge.
Et pour égal en valeur absolue à ce rayon, on ne sait pas.

Ici, peut être réel ou complexe (remplacer "valeur absolue" par "module").

Exemples :
La série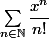 a pour rayon de convergence l'infini, donc converge absolument pour tout x (réel ou complexe). La somme est d'ailleurs égale à

La série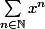 a pour rayon de convergence 1. Si 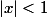, la série converge, cela peut se voir facilement car c'est la limite de la somme des termes d'une suite géométrique de raison et la somme est .
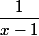Mais pour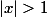 , la série diverge grossièrement. Et pour 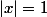il n'y a pas convergence non plus (limite infinie pour , pas de limite du tout sinon)

[moijesuissansE]

D'accord, j'ai saisi, Merci BEAUCOUP !!!!