Fonction dans un nouveau repère
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Thomas210
- Messages: 5
- Enregistré le: 15 Avr 2021, 17:51
-
 par Thomas210 » 30 Mai 2021, 16:00
par Thomas210 » 30 Mai 2021, 16:00
Voici le problème (question 2):

Merci infiniment
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 30 Mai 2021, 16:07
par Pisigma » 30 Mai 2021, 16:07
Bonjour,
A vos ordres mon Colonnel!!
-
mathou13
- Membre Relatif
- Messages: 204
- Enregistré le: 08 Juin 2019, 14:52
-
 par mathou13 » 30 Mai 2021, 21:15
par mathou13 » 30 Mai 2021, 21:15
Bonjour,
1)a)
f(x)=(2x^2-7x+8)/(x-2)
f est définit sur R\{2}
f'(x)=((4x-7)*(x-2)-(2x^2-7x+8)*1)/(x-2)^2
= ( 2x^2-8x+6)/(x-2)^2
x_______________/-infini______1_______2____________3______+infini
x-2____________/__________-_______-___0_______+_______+_
(x-2)^2_______/____+_________________//__________________
2x^2-8x+6__/_________+____0_____-_//__-_________0____+_
f'(x)_________/_________+____0_____-_//___-_________0____+__
Cf__________/__croissante_max_dé//croissante__min_local_croissante__(le max est local)
2x^2-7x+8___/_____+________________+________
f(x)___________/______-_________//______+__________
Cf_________/en dessous de 0_//__au dessus de 0_____
b) y=2x-3
f(x)-(2x-3)=(2x^2-7x+8)/(x-2) - (2x-3)=((2x^2-7x+8) - (2x-3)(x-2))/(x-2)=(2)/(x-2)
lim(x->+-infini) f(x)-(2x-3)=0 (car constante/+-infini->0)
c)
tableau de valeur
asymptote y=2x-3 et x=2 min (3;f(3)) et max local (1;f(1))
Vous pouvez tracer avec ces éléments et le tableau de variation.
2)
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 30 Mai 2021, 21:29
par Pisigma » 30 Mai 2021, 21:29
Bonjour matou13,
malgré son style..., je crois que Thomas210 attendait une réponse pour le point 2
-
mathelot
 par mathelot » 31 Mai 2021, 17:38
par mathelot » 31 Mai 2021, 17:38
bonsoir,
le but est de calculer les anciennes coordonnées (x;y) en fonction des nouvelles (X;Y) de manière à pouvoir remplacer x et y dans l'ancienne équation par leurs expressions en fonction de X et Y, pour obtenir la nouvelle équation Y=2/X
le changement de repère donne:
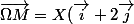+Y \vec{j}=\vec{OM}-\vec{O \Omega}=x\vec{i}+y\vec{j}-2 \vec{i}-\vec{j})
Ensuite , on égalise, de par et d'autre du signe égal, les coordonnées dans la base
)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
