Bonjour,
Est-ce que:
(1/2n)[(2n)!]/[(4^n)n!] = (1/n)[1/(2n+1)](2n+2)! / [4^(n+1)](n+1)!
?
C'est ce que je trouve alors que je suis sensé trouver:
(1/2n)[(2n)!] / [(4^n)n!] = [1/(2n+1)](2n+2)! / [4^(n+1)](n+1)!
Calcul
9 messages
- Page 1 sur 1
Re: calcul
D'accord, j'ai essayé pour n=2 et j'en déduis que c'est la première formule qui est exacte.
Re: calcul
Bonjour,
De façon à bien comprendre la question, pour la deuxième égalité les deux expressions sont elles les suivantes ?
!}{4^n . n!})
et
!}{4^{n+1} .(n+1)!})
De façon à bien comprendre la question, pour la deuxième égalité les deux expressions sont elles les suivantes ?
et
Re: calcul
Si c'est bien ce que j'ai écrit,
si on enlève le n du dénominateur de la première fraction l'égalité est juste sinon elle est fausse.
C'est à dire écrire au lieu de
au lieu de 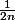 .
.
si on enlève le n du dénominateur de la première fraction l'égalité est juste sinon elle est fausse.
C'est à dire écrire
Re: calcul
Oui c'est bien ça. En fait, voici mon pbm:
Pour tout n sup ou égal à 1 , il existe une fct A[n] telle que pour tout x sup à 0 : A[n+1](x)=-A[n]'(x)/n
Je dois faire une récurrence pour montrer que
pour tout n sup ou égal à 1 , pour tout x sup à 0 :
A[n](x) = ( (1/2n-1)[(2n)!]/[(4^n)n!] ) x^[-(2n-1)/2]
On suppose l'initialisation vérifiée.
Je suppose pour un rang n que: A[n](x) = ( (1/2n-1)[(2n)!]/[(4^n)n!] ) x^[-(2n-1)/2]
Je dérive et j'obtiens: A[n]'(x) = -( (1/2)[(2n)!]/[(4^n)n!] ) x^[-(2n+1)/2]
Donc, avec la relation A[n+1](x)=-A[n]'(x)/n , je trouve:
A[n+1](x) = ( (1/2n)[(2n)!]/[(4^n)n!] ) x^[-(2n+1)/2]
=(1/n)[1/(2n+1)](2n+2)! / ( [4^(n+1)](n+1)! ) x^[-(2n+1)/2]
Le (1/n) est en trop... Je ne vois pas où je fais une erreur. Dans ma dérivée de A[n]?
Pour tout n sup ou égal à 1 , il existe une fct A[n] telle que pour tout x sup à 0 : A[n+1](x)=-A[n]'(x)/n
Je dois faire une récurrence pour montrer que
pour tout n sup ou égal à 1 , pour tout x sup à 0 :
A[n](x) = ( (1/2n-1)[(2n)!]/[(4^n)n!] ) x^[-(2n-1)/2]
On suppose l'initialisation vérifiée.
Je suppose pour un rang n que: A[n](x) = ( (1/2n-1)[(2n)!]/[(4^n)n!] ) x^[-(2n-1)/2]
Je dérive et j'obtiens: A[n]'(x) = -( (1/2)[(2n)!]/[(4^n)n!] ) x^[-(2n+1)/2]
Donc, avec la relation A[n+1](x)=-A[n]'(x)/n , je trouve:
A[n+1](x) = ( (1/2n)[(2n)!]/[(4^n)n!] ) x^[-(2n+1)/2]
=(1/n)[1/(2n+1)](2n+2)! / ( [4^(n+1)](n+1)! ) x^[-(2n+1)/2]
Le (1/n) est en trop... Je ne vois pas où je fais une erreur. Dans ma dérivée de A[n]?
Re: calcul
Personnellement je ferai ainsi :
!}{4^{n+1}(n+1)!}=\frac{1}{2n+1}\times\frac{(2n+2)(2n+1)(2n)!}{4^n\times 4\times(n+1)n!}=\frac{(2n)!}{2\times 4^n\times n!})
Avec simplification par (2n+1) et par 2n+2 ou plutôt 2(n+1).
Avec simplification par (2n+1) et par 2n+2 ou plutôt 2(n+1).
Re: calcul
Oui c'est bien ça. En fait, voici mon pbm:
Pour tout n sup ou égal à 1 , soit une fct A[n] telle que pour tout x sup à 0 : A[n+1](x)=-A[n]'(x)/n
Je dois faire une récurrence pour montrer que
pour tout n sup ou égal à 1 , pour tout x sup à 0 :
A[n](x) = ( (2n)!/(2n-1) / [(4^n)n!] ) x^[-(2n-1)/2]
On suppose l'initialisation vérifiée (à n=1).
Je suppose pour un rang n que: A[n](x) = ( (2n)!/(2n-1) / [(4^n)n!] ) x^[-(2n-1)/2]
Je dérive et j'obtiens: A[n]'(x) = -( (2n)!/[2(4^n)n!] ) x^[-(2n+1)/2]
Donc, avec la relation A[n+1](x)=-A[n]'(x)/n , je trouve:
A[n+1](x) = (1/n) ( [(2n)!/[2(4^n)n!] ) x^[-(2n+1)/2]
= (1/n) (1/(2n+1)) (2n+2)! / (4^(n+1)(n+1)!] ) x^[-(2n+1)/2]
Le (1/n) est en trop... Je ne vois pas où je fais une erreur. Dans ma dérivée de A[n]?
Pour tout n sup ou égal à 1 , soit une fct A[n] telle que pour tout x sup à 0 : A[n+1](x)=-A[n]'(x)/n
Je dois faire une récurrence pour montrer que
pour tout n sup ou égal à 1 , pour tout x sup à 0 :
A[n](x) = ( (2n)!/(2n-1) / [(4^n)n!] ) x^[-(2n-1)/2]
On suppose l'initialisation vérifiée (à n=1).
Je suppose pour un rang n que: A[n](x) = ( (2n)!/(2n-1) / [(4^n)n!] ) x^[-(2n-1)/2]
Je dérive et j'obtiens: A[n]'(x) = -( (2n)!/[2(4^n)n!] ) x^[-(2n+1)/2]
Donc, avec la relation A[n+1](x)=-A[n]'(x)/n , je trouve:
A[n+1](x) = (1/n) ( [(2n)!/[2(4^n)n!] ) x^[-(2n+1)/2]
= (1/n) (1/(2n+1)) (2n+2)! / (4^(n+1)(n+1)!] ) x^[-(2n+1)/2]
Le (1/n) est en trop... Je ne vois pas où je fais une erreur. Dans ma dérivée de A[n]?
Re: calcul
Oui je pense que la division par n est en trop dans la définition A[n+1](x)=-A[n]'(x)/n
Si on essaye A[n+1](x)=-A[n]'(x) pour n=1 puis n=2, c'est correct idem pour le cas général.
Si on essaye A[n+1](x)=-A[n]'(x) pour n=1 puis n=2, c'est correct idem pour le cas général.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
