Bonjour,
J'ai un exo à faire et dans une question on me demande:
Démontrer que (a+b)^p = a^p + b^p + kp puis en déduire que 2^p= 2+kp avec k dans Z et p premier
Démontrer que n^p = n + k' p et que p divise n(n^(p-1)-1).
Je suis parti du binome de Newton mais j'ai pas abouti donc je bloque pour le reste des questions
Merci à vous.
Fermat
4 messages
- Page 1 sur 1
Re: Fermat
par capitaine nuggets » 20 Avr 2021, 11:15
Salut !
^p=\sum_{k=0}^p \binom p k a^k b^{p-k})
Que vaut le terme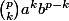
lorsque 
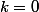? Lorsque 
?
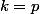Montre que dès que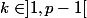
, 
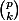est toujours un multiple de 
.
Que vaut le terme
Montre que dès que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Fermat
par Bob1sérieux » 23 Avr 2021, 17:01
Merci beaucoup,
J'ai trouvé,
Il me manque que
"Démontrer que n^p = n + k' p et que p divise n(n^(p-1)-1)."
Si vous pouviez m'aider svp,
J'ai trouvé,
Il me manque que
"Démontrer que n^p = n + k' p et que p divise n(n^(p-1)-1)."
Si vous pouviez m'aider svp,
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :