Logique

[pierrelouisbourgeois]

Bonjour,

Savez si il est possible de démontrer cette équivalence sans tables de vérité ?
(en fait en utilisant que les connecteurs comme la négation, le "et", "ou", avec les lois de Morgan)

L'équivalence est : P et (Q ou R) ⇔ (P et Q) ou (P et R)

Merci à vous.

[hdci]

Bonjour,
On peut assimiler les lois de Morgan avec la théorie des ensembles, "Et" représentant l'intersection et "ou" la réunion.
si P,Q,R soit trois ensembles,


On peut alors démontrer simplement cette égalité en considérant un élément de l'ensemble de gauche et vérifier qu'il appartient à l'ensemble de droite, et réciproquement.

Le lien avec les propositions est le suivant : si p est une proposition, l'ensemble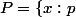 est très exactement l'ensemble des objets x pour lesquels p est vraie.
(Je fais abstraction ici de la théorie naïve vs théorie ZFC des ensembles, pour éviter d'entrer dans une théorie contradictoire il faudrait parler d'un sur-ensemble).

A noter : cela fonctionne si P,Q,R sont des propositions en fonction d'une variable x.

[pierrelouisbourgeois]

Merci pour votre réponse.