Intégrales et primitives

[Vava03]

Bonsoir,
Est-ce que quelqu'un pourrait m'aider pour déterminer la primitive de ln(x) et la primitive ln(x)². Je ne vois pas comment on fait.
Merci d'avance.

[phyelec]

bonjour,

la primitive de ln(x) est xln(x)-x
je vous laisse un peu chercher pour l'autre

[mathelot]

bonjour,
on pose comme primitive



et on intègre par parties, en posant et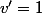

on a donc
à intégrer par parties.

rappel de cours:
soient u,v deux fonctions réelles intégrables et de dérivées intégrables sur un intervalle ouvert non vide:
on a la formule de dérivée d'un produit de deux fonctions:

en terme de primitives , cela donne:



soit:

[Vava03]

Ah d'accord merci beaucoup !

[mathelot]

est ce que tu peux publier ton résultat de la primitive de qu'on voit si c'est juste ?

sinon, tu peux toujours dériver le résultat et voir si l'on retombe sur