Fonction dérivée

[pololoco]

Bonjour, je n'arrive pas à réaliser cet exercice, j'ai pourtant cherché, mais je n'arrive pas.
Pouvez-vous m'aider s'il vous plaît.

[hdci]

Bonjour,

Vous avez écrit

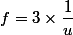
Ce qui est un bon début.

Je ne vois pas très bien ce que vous avez fait ensuite ; il y a des éléments "épars" mais je ne vois pas la cohérence du tout.

Quelle est la dérive de (1/u) ? C'est une formule de votre cours.

[mathou13]

Bonjour,

f(x)=- 3 / (x^2+2x+4)=-3/u(x) (avec u(x)=x^2+2x+4)
f'(x)=-3*(-1)*u'(x)*u(x)^(-1-1)=3*(2x+2)/(x^2+2x+4)^2=6(x+1)/(x^2+2x+4)^2

rq: si f(x)=u(x)^n (n dans N) alors f(x)=n*u'(x)*u(x)^(n-1)

[Black Jack]

Bonjour,

Le piège ... peut-être

... est que l'énoncé demande de laisser le dénominateur sous forme factorisée ... alors que celui-ci n'est pas factorisable (du moins dans R).

[hdci]

Dans IR, le dénominateur de la dérivée est bien sous forme factorisée ; carré d'un polynôme irréductible.

Je pense que l'énoncé demande juste à ne pas développer ce carré.