Equation avec sinus de matrice

[Restefond34]

Bonjour à tous,

je suis en MP et cherche les matrices telles que
On constate déjà que est déjà trigonalisée, mais non diagonalisable quand . En trigonalisant l'inconnue , on voit que les valeurs propres doivent être de la forme , mais cela ne suffit évidemment pas à conclure sur .
Une autre idée qui m'est venue est d'écrire avec diagonalisable, nilpotente et . Ensuite, j'écris en réarrangeant (et sachant que

J'ai envie de dire que est diagonalisable, et que est nilpotente et ensuite j'aimerai utiliser l'unicité de la décomposition diagonalisable+nilpotente avec la matrice , mais je n'ai pas l'impression que l'identification soit simple...

Auriez-vous des pistes ou des commentaires ?
Excellente journée !

[GaBuZoMeu]

Bonjour,

Si est une matrice diagonale, que peux-tu dire de ?

[Restefond34]

Bonjour,

merci pour votre réponse qui m'a un peu débloqué !
Si est diagonale, je peux dire que est diagonale. De même, si j'ai , alors, en raisonnant comme par linéarité et continuité de produit matriciel, j'ai
De même,
Donc cela confirme bien que est diagonalisable !

Et ensuite, j'identifie à (dans mon cas, j'ai dans la décomposition diagonalisable+nilpotente) donc j'en déduis les deux valeurs de et qui sont congrues à .
Ensuite, mon impression, c'est que est nulle, donc on n'a pas de partie nilpotente.

En conclusion, si , je n'ai pas de solution.
Mais si , j'ai toutes les matrices semblables à celles avec et .
J'ai l'impression de manquer quelque chose pour le cas ... Voyez-vous où ?

[GaBuZoMeu]

Je pense que tu as tout dit, non ?
Si ça peut te rassurer, quelques questions :
Si , peut-on avoir une solution diagonalisable ?
Si n'est pas diagonalisable, que peux-tu dire de ses valeurs propres ?
Que vaut le sinus de ?

[Restefond34]

En effet, il me semble que ça marche !
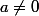
Donc si , pas de solutions.
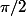
Si , je n'ai aucune condition sur si ce n'est qu'elle comute avec . En définitive, toute matrice somme d'une matrice diagonalisable à valeurs propres congrues à et d'une matrice nilpotente (qui commute avec la première matrice dz) est solution !

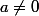
Si , pas de solutions, on ne peut pas avoir de solution diagonalisable ( le serait).
Si n'est pas diagonalisable, ses deux valeurs propres (ici) sont égales, elle est donc semblable à la matrice que vous proposez dont le sinus vaut (sauf erreur...)
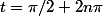
J'obtiens à nouveau l'identification (cette fois, une seule vp !) et donc , ce qui pose problème ! Donc cela confirme qu'il n'y a pas de solutions !

Mais si , avec ce raisonnement, j'obtiens que est juste diagonalisable avec les vp qui vont bien. Mais je ne peux pas rajouter ma matrice nilpotente comme j'avais fait précédemment...
EDIT : En fait, si , rien ne dit que est diagonalisable, donc je me ramène à la décompo précédente et c'est bon !