Dérivée
6 messages
- Page 1 sur 1
 Dérivée
Dérivée
Bonjour je voudrais savoir si quelqu'un peut m'aider à comprendre comment la dérivée de racine carré de x. Sur ma leçon c'est écrit que c'est égale à 1 sur 2 racine carré de x mais je ne comprend pas comment on obtient ce résultat et en cherchant sur internet je trouve des trucs avec des h auquel on ne parle pas en cours donc je suis vraiment perdu. Si quelqu'un peut m'aider merci d'avance
Re: Dérivée
Bonjour,
Qu'avez-vous vu en cours ?
La définition du nombre dérivé de la fonction f, pour x=a, c'est
-f(a)}{h})
C'est-à-dire, quand on prend des nombres h "très très très proches de zéro", l'expression se "stabilise" en un nombre donné.
D'un point de vue plus "concret", c'est le calcul de la vitesse instantanée : si vous parcourez en une seconde une distance de 10 mètres, votre vitesse moyenne, pendant cette seconde, est de 10 mètres par seconde, mais elle n'a pas forcément été constante pendant toute la seconde. Donc pour calculer une vitesse "plus précise", il faut prendre un intervalle de temps "plus court", sauf que ce sera toujours une vitesse moyenne (sur un délai très court c'est vrai, mais...). La vitesse instantanée devrait être alors calculée sur un délai nul, mais on ne peut pas diviser par zéro : d'où cette notion de limite.
Exemple : avec la fonction carré, le nombre dérivé en 2 est^2-2^2}{h}) . Mais ça on sait le calculer très précisément, car pour h non nul, on a
. Mais ça on sait le calculer très précisément, car pour h non nul, on a
^2-2^2}{h}=4+h)
Et quand h "tend vers zéro", 4+h "tend vers 4" (remplacer "tendre" par "s'approcher" pour comprendre le concept). Donc le nombre dérivé de la fonction carré en 2 est 4, et si on fait cela pour n'importe quel nombre x, on voit que cela fait 2x.
On procède de même pour la racine carrée, mais les calculs sont plus subtils : on multiplie par la quantité conjuguée pour simplifier le numérateur. Pour x non nul cela donne
(\sqrt{x+h}+\sqrt{x})}{h(\sqrt{x+h}+\sqrt{x})}=\dfrac{x+h-x}{h(\sqrt{x+h}+\sqrt{x})}=\dfrac{1}{\sqrt{x+h}+\sqrt{x}})
Quand h tend vers (s'approche de) zéro, le numérateur ne change pas, le dénominateur tend vers (s'approche de)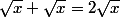
D'où le résultat.
Qu'avez-vous vu en cours ?
La définition du nombre dérivé de la fonction f, pour x=a, c'est
C'est-à-dire, quand on prend des nombres h "très très très proches de zéro", l'expression se "stabilise" en un nombre donné.
D'un point de vue plus "concret", c'est le calcul de la vitesse instantanée : si vous parcourez en une seconde une distance de 10 mètres, votre vitesse moyenne, pendant cette seconde, est de 10 mètres par seconde, mais elle n'a pas forcément été constante pendant toute la seconde. Donc pour calculer une vitesse "plus précise", il faut prendre un intervalle de temps "plus court", sauf que ce sera toujours une vitesse moyenne (sur un délai très court c'est vrai, mais...). La vitesse instantanée devrait être alors calculée sur un délai nul, mais on ne peut pas diviser par zéro : d'où cette notion de limite.
Exemple : avec la fonction carré, le nombre dérivé en 2 est
Et quand h "tend vers zéro", 4+h "tend vers 4" (remplacer "tendre" par "s'approcher" pour comprendre le concept). Donc le nombre dérivé de la fonction carré en 2 est 4, et si on fait cela pour n'importe quel nombre x, on voit que cela fait 2x.
On procède de même pour la racine carrée, mais les calculs sont plus subtils : on multiplie par la quantité conjuguée pour simplifier le numérateur. Pour x non nul cela donne
Quand h tend vers (s'approche de) zéro, le numérateur ne change pas, le dénominateur tend vers (s'approche de)
D'où le résultat.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Dérivée
Bonjour,
hdci a fait une belle démonstration mais si tu n’as pas vu cela en cours ou si tu veux juste le retrouver rapidement en pratique, tu peux te contenter de retenir que la dérivée de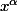 pour
pour  constante réelle est
constante réelle est 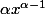
Or, on peut écrire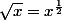 donc la dérivée est
donc la dérivée est 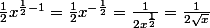
hdci a fait une belle démonstration mais si tu n’as pas vu cela en cours ou si tu veux juste le retrouver rapidement en pratique, tu peux te contenter de retenir que la dérivée de
Or, on peut écrire
Re: Dérivée
Merci c'est beaucoup plus clair, je viens de comprendre. Donc racine carré et puissance de 1/2 c'est la même chose au final. Y a juste le 1/2 qui se transforme en 2 que je vois pas trop ce qu'il fait là mais j'ai juste à retenir qu'il est la quoi. Merci beaucoup
Re: Dérivée
Il ne s'agit pas de retenir des recettes, il faut comprendre.
Que se passe-t-il quand tu remplaces par
par  dans le post de Vassillia ?
dans le post de Vassillia ?
Que se passe-t-il quand tu remplaces
Re: Dérivée
Le 1/2 ne se transforme pas en 2 enfin je vois ce que tu veux dire mais c'est parfaitement logique, je détaille le passage qui semble poser problème :
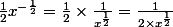
Edit : désolée pas vu ta réponse avant de poster Sa majesté
Edit : désolée pas vu ta réponse avant de poster Sa majesté

6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
