Polynôme caractéristique dimension 3

[jeje56]

Bonjour à tous,
L'objectif est d'exprimer le deuxième coefficient du polynôme caractéristique d'une matrice A de dimension 3 en fonction de la trace de A : .
Un exercice préalable est de trouver le résultat pour une matrice A diagonale, l'idée étant de généraliser ensuite à toute matrice carrée .
Avez-vous des pistes à me conseiller ?
Merci !

[GaBuZoMeu]

Bonjour,

En fonction uniquement de la trace de , c'est impossible. Relis bien ton énoncé. N'est-ce pas plutôt en fonction des traces de et de ?

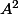
[jeje56]

Oui GaBu, en fait je connais la réponse : .

[GaBuZoMeu]

Ben alors, pourquoi donnes-tu un énoncé faux ?

As-tu regardé ce qui se passe pour une matrice diagonale ?

[jeje56]

Ben alors, pourquoi donnes-tu un énoncé faux ?

Peut-être parce que l'erreur est humaine non ?! Tu ne laisses rien passer toi hein !

[GaBuZoMeu]

As-tu regardé ce qui se passe pour une matrice diagonale ?

[jeje56]

Si a, b et c sont les éléments diagonaux d'une matrice diagonale D : ...

[jeje56]

Et : ça fonctionne.

[GaBuZoMeu]

Il ne te reste plus qu'à passer du cas diagonal au cas général.
Une façon de faire est de commencer par le cas triangulaire ....

[jeje56]

J'aurais tendance à généraliser le résultat à toute matrice diagonalisable puisque les traces de matrices semblables sont égales... Mais pour la généralisation à toute matrice carrée je bloque...

[GaBuZoMeu]

Une façon de faire est de commencer par le cas triangulaire ....

Je sors, il y a match.

[Vassillia]

Désolé pour le total hors sujet mais beau match et on ne pourra pas dire qu'il n'y a pas eu de suspens, bravo aux anglais.

[jeje56]

Une façon de faire est de commencer par le cas triangulaire ....

Cas triangulaire similaire au cas diagonal : ça fonctionne...
Pour généraliser : toute matrice réelle est trigonalisable dans et les traces de matrices semblables sont égales... Mais qu'en est-il des traces des carrés de matrices semblables ?...
Edit : Les carrés de matrices semblables sont semblables... Donc leurs traces sont égales. D'où la généralisation à toute matrice d'ordre 3.
Mon raisonnement est-il correct ?
Merci !

[GaBuZoMeu]

Presque : ce n'est pas vrai que toute matrice est trigonalisable sur .

[jeje56]

Presque : ce n'est pas vrai que toute matrice est trigonalisable sur .

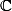
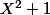
C'est exactement ce qui me chiffonne... Toute matrice est trigonalisable sur , les valeurs propres pouvant ne pas être réelles à l'image de i et -i pour un polynôme caractéristique égal à de la matrice réelle A=((0 ; -1), (1 ; 0)) par exemple...

[GaBuZoMeu]

Pourquoi est-ce que ça te chiffonne ?

[jeje56]

Pourquoi est-ce que ça te chiffonne ?

Je voulais dire que je n'étais plus sûr de cette affirmation...
Bel exercice je trouve ! Une suite serait de regarder ce qu'il se passe pour les coefficients du polynôme caractéristique à un ordre supérieur...

[GaBuZoMeu]

Je ne comprends pas ta réponse. De quelle affirmation parles-tu ?

Pour la suite, voir les identités de Newton entre sommes de puissances et polynômes symétriques élémentaires.
https://fr.wikipedia.org/wiki/Identit%C3%A9s_de_Newton

[jeje56]

Bonjour,
En relisant le raisonnement quelque chose m'échappe...
On a montré que le coefficient en t du polynôme caractéristique d'une matrice 3*3 triangulaire T est .
Je ne vois plus comment en déduire que le coefficient en t du polynôme caractéristique d'une matrice 3*3 quelconque A est ...
Merci de votre aide !