Ca ressemble à de la topologie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par Alien Life Form » 08 Déc 2006, 17:45
par Alien Life Form » 08 Déc 2006, 17:45
Soit

un ensemble a priori quelconque.
Soit f :
 \rightarrow P(E))
une fonction totale telle que :
-
)
-
) = f(e))
-
 = \bigcup_{i \in I} f\left(e_i\right))
(*)
-
=\emptyset)
Est-ce que la propriété suivante est vraie ?
pour tout
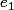
et
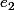
finis il existe un
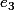
fini tel que :
 \cap f(e_2) = f(e_3)) correction
correction : (*) en remplacement de
 = f(e_1) \cup f(e_2))
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Déc 2006, 17:52
par yos » 08 Déc 2006, 17:52
Bonsoir
Alien Life Form a écrit:Soit f :
 \rightarrow P(E))
une fonction totale telle que :
C'est quoi la définition de ceci?
 par Alien Life Form » 08 Déc 2006, 17:56
par Alien Life Form » 08 Déc 2006, 17:56
Une fonction des parties de E dans les parties de E
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Déc 2006, 18:01
par yos » 08 Déc 2006, 18:01
OK alors le mot "totale" était décoratif.
Je vais regarder.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Déc 2006, 18:13
par yos » 08 Déc 2006, 18:13
A mon avis c'est vrai (car je trouve pas de contre-exemple...).
f est définie par l'image des singletons. On peut voir f de E dans P(E).
Je vais chercher un argument...
à mon avis

est un bon candidat pour
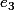
.
 par Alien Life Form » 08 Déc 2006, 20:01
par Alien Life Form » 08 Déc 2006, 20:01
j'avais pensé à cette eventualité mais

ne marche pas pour
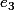
Si on prend

et si
)
est l'ensemble des nombres divisibles par un element de

(càd
=\{k \in \mathbb{N}^*)
tq

) alors
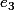
se calcule en fonction des ppcm entre
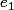
et
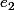
.
Typiquement
 \cap f(\{3;5\})=f(\{6;10\}))
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Déc 2006, 20:36
par yos » 08 Déc 2006, 20:36
Ouais, j'ai pas été très prudent.
Il faudrait regarder
\cap f(e_2)\right))
qui est aussi
\right)\cap f^{-1}\left(f(e_2)\right))
, et sa finitude.
 par Alien Life Form » 08 Déc 2006, 22:19
par Alien Life Form » 08 Déc 2006, 22:19
Là je ne te suis plus, j'ai dû louper une marche.
Si on reprend l'exemple précédent
) = \{ e \in P(n.{\mathbb N}) \text{ tq } n \in e\})
(c.à.d. l'ensemble des parties des multiples de

qui contiennent

)
d'où si
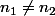
:
-
 \cap f\left(\{n_2\})\right) = f^{-1} \left(f\left(\{ppcm(n_1,n_2)\}\right)\right))
non vide (et infini)
-
\right) \cap f^{-1}\left(f\left(\{n_2\}\right)\right) = \emptyset)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 08 Déc 2006, 22:55
par yos » 08 Déc 2006, 22:55
J'ai utilisé l'égalité générale
=f^{-1}(A)\cap f^{-1}(B))
... qui est toujours vraie ... mais pas ici ... parce que l'intersection est ici une loi interne sur les éléments de l'ensemble de départ de f.
Bon voilà je m'embrouille.
Je vais regarder de plus près mais c'est déroutant comme problème.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 08 Déc 2006, 23:39
par fahr451 » 08 Déc 2006, 23:39
yos je ne vois pas pourquoi f est définie par l'image des singletons;par la propriété de f l'image d 'une union de deux parties et donc d un nbre fini est l 'union des images; mais une partie qq est une union qq de ses singletons . donc l'image de cette union n'est pas a priori l'union des images. non ?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Déc 2006, 00:01
par fahr451 » 09 Déc 2006, 00:01
je me trompe où f = identité de P(E)?
on a pourA une partie de E , inclus ds f(A) (hypothèse 1)
on en déduit pour f(A) , f(A) inclus ds f(f(A)) ; or lhypothèse 2 donne f(f(A)) = A , donc f(A) = A
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Déc 2006, 00:14
par tize » 09 Déc 2006, 00:14
fahr451 a écrit:je me trompe où f = identité de P(E)?
on a pourA une partie de E , inclus ds f(A) (hypothèse 1)
on en déduit pour f(A) , f(A) inclus ds f(f(A)) ; or lhypothèse 2 donne f(f(A)) = A , donc f(A) = A
Attention l'hypothèse 2 affirme f(f(A))=f(A) !
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Déc 2006, 00:16
par yos » 09 Déc 2006, 00:16
L'application

semble convenir pourtant (on peut la définir par les images des singletons même si , comme tu me le faisais remarquer, ce n'est pas toujours le cas), donc je vois pas pourquoi f serait l'identité.
Tu fais, je pense, la même erreur que moi avec les intersections. f(A) est un élément de P(E) et pas une partie.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Déc 2006, 00:17
par fahr451 » 09 Déc 2006, 00:17
je lis pas l 'énoncé correctement ( bis)
ronchtulu !
"mon" hypothèse 2 bis avait le mérite d'être cool mais ce n'est pas celle de l'énoncé
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Déc 2006, 00:29
par tize » 09 Déc 2006, 00:29
Bon je me lance quitte à dire une grosse bêtise :
voilà comment je vois les choses, f est une application totale qui "croit" et dont l'image d'un élément est un élément stable par f (prop.2).
On nous dit de plus que l'union de 2 éléments stables par f est encore stable par f (prop.3) , soit :
 \cap f(e_2) = f(e_3))
, je pense que le
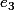
en question n'est autre que
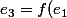 \cap f(e_2))
, et on veut montrer en réalité que l'intersection de 2 éléments stable est encore stables. Avec (prop. 1) on a
 \cap f(e_2)\subset f(f(e_1) \cap f(e_2)))
, reste à montrer que
 \cap f(e_2))\subset f(e_1) \cap f(e_2))
.
Soit donc
 \cap f(e_2)))
, il existe alors
 \cap f(e_2))
tel que
\subset f(f(e_1))=f(e_1))
.
De même
)
donc
\cap f(e_2))
d'ou :
 \cap f(e_2))
et on a bien l'égalité cherché...
En suivant mon raisonnement, soit j'ai bon soit j'ai dit une grosse connerie...qu'en pensez-vous (soyez indulgents...)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Déc 2006, 00:30
par tize » 09 Déc 2006, 00:30
Bon je me lance quitte à dire une grosse bêtise :
voilà comment je vois les choses, f est une application totale qui "croit" et dont l'image d'un élément est un élément stable par f (prop.2).
On nous dit de plus que l'union de 2 éléments stables par f est encore stable par f (prop.3) , soit :
 \cap f(e_2) = f(e_3))
, je pense que le
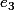
en question n'est autre que
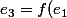 \cap f(e_2))
, et on veut montrer en réalité que l'intersection de 2 éléments stable est encore stables. Avec (prop. 1) on a
 \cap f(e_2)\subset f(f(e_1) \cap f(e_2)))
, reste à montrer que
 \cap f(e_2))\subset f(e_1) \cap f(e_2))
.
Soit donc
 \cap f(e_2)))
, il existe alors
 \cap f(e_2))
tel que
\subset f(f(e_1))=f(e_1))
.
De même
)
donc
\cap f(e_2))
d'ou :
 \cap f(e_2))
et on a bien l'égalité cherché...
En suivant mon raisonnement, soit j'ai bon soit j'ai dit une grosse connerie...qu'en pensez-vous (soyez indulgents...)
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 09 Déc 2006, 00:39
par yos » 09 Déc 2006, 00:39
Trop fatigué pour réfléchir.
Juste une remarque : la proposition 2 dit que l'image d'un élément est un point fixe de f et c'est pas pareil que de la stabilité.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Déc 2006, 00:42
par tize » 09 Déc 2006, 00:42
yos a écrit:Trop fatigué pour réfléchir.
Juste une remarque : la proposition 2 dit que l'image d'un élément est un point fixe de f et c'est pas pareil que de la stabilité.
Oui, c'est vrai, j'ai appelé ça comme ça sur le coup....stable n'est pas le terme le plus adéquat...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 09 Déc 2006, 00:44
par fahr451 » 09 Déc 2006, 00:44
je ne saisis pas le passage de x appartient à f(A) à il existe y appartenant à A tel que x appartient à f(y) [A étant f(e1) inter f(e2)]
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Déc 2006, 00:55
par tize » 09 Déc 2006, 00:55
fahr451 a écrit:je ne saisis pas le passage de x appartient à f(A) à il existe y appartenant à A tel que x appartient à f(y) [A étant f(e1) inter f(e2)]
Je m'explique :
\cap f(e_2))=f\(\bigcup\limits_{y\in f(e_1)\cap f(e_2)}\{y\}\)=\bigcup\limits_{y\in f(e_1)\cap f(e_2)}f(\{y\}))
d'après (prop.3)...non ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités