Résolution système d'équation (complexe)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Malekit68
- Messages: 2
- Enregistré le: 11 Mar 2021, 17:03
-
 par Malekit68 » 11 Mar 2021, 17:13
par Malekit68 » 11 Mar 2021, 17:13
Bonjour à tous,
Je bloque sur un système d'équation :
~~~~ r = A.cos(\phi))
~~~~ r = \frac{B}{\theta.tan(\phi)})
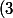~~~~ r = \frac{C}{sin(\theta)})
Est-il possible de le résoudre sans passer par des approximations itératives ?
Me manque-t-il quelque chose ?
Je précise que A, B et C sont des constantes, et que

et

sont compris entre

et
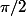
.
Un grand merci pour votre aide

-
mathelot
 par mathelot » 11 Mar 2021, 18:00
par mathelot » 11 Mar 2021, 18:00
bonjour,
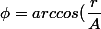)
calculons
=\dfrac{\sqrt{1-cos^2(x)}}{cos(x)})
=\dfrac{\sqrt{1-x^2}}{x})
l'égalité (2) donne:
)}=\dfrac{Br}{\theta. \sqrt{A^2-r^2}})

l'égalité (3) donne une équation d'inconnue r:
=C)
je me demande si cette dernière équation admet des solutions, il faudrait voir avec des valeurs numériques pour A,B et C
-
Malekit68
- Messages: 2
- Enregistré le: 11 Mar 2021, 17:03
-
 par Malekit68 » 11 Mar 2021, 20:44
par Malekit68 » 11 Mar 2021, 20:44
Merci pour la réponse !
Je pense qu'il n'y a pas moyen de trouver de solutions simplement (sans itérations). J'ai donc contourné le problème en fixant r.
Je vais pas rentrer dans les détails c'est de la physique des particules, mais encore merci pour votre aide !
-
mathelot
 par mathelot » 11 Mar 2021, 21:24
par mathelot » 11 Mar 2021, 21:24
l'égalité (3) donne une équation d'inconnue r:
=C)
je me demande si cette dernière équation admet des solutions, il faudrait voir avec des valeurs numériques pour A,B et C
r ne peut pas tendre vers 0 sinon C serait nulle. Si r tend vers A (par valeurs inférieures à A), le sinus oscille entre -1 et 1 et si |C| est inférieur à |A| , on a une infinité de solutions.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités