Aide pour une somme d'une suite

[Murnight13]

Bonjour,

Je demande votre aide car je n'arrive pas à trouver une formule qui fonctionne pour une suite.
Voici la suite en question:

exp^(-3) * [(3^x)/(x!)]

Cela est sans doute une question bête mais je n'ai trouver aucune aide sur internet, je me tourne vers vous

Merci d'avance

[Rhaegar]

Bonjour,

Je ne comprends pas ta question, peux-tu être plus clair ?

[Murnight13]

Bonjour,

En ce moment, je fais la loi de Poisson en cours. Dans ce dernier il existe la formule : exp^(lambda) * [(lambda^-k) / (k!)]

Dans des exercices, nous sommes parfois amené à devoir calculer cette expression pour k=0, k=1,... et à en faire la somme. Seulement, plutôt que de calculer à chaque fois pour chaque valeur de k, je me demande si il ne serait pas possible de calculer la somme des termes de cette formule en la mettant sous forme de suite.

[GaBuZoMeu]

Bonjour,

Un petit conseil : revois ta formule pour la loi de Poisson.

Ensuite, ne connais-tu pas la formule ?

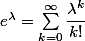
[Murnight13]

je pense que vous n'avez pas compris ma demande./ Mais peut-être est-ce moi qui m'enfonce dans une niche / idiotie

Bonne continuation à vous

[hdci]

Si vous voulez une "formule" pour simplifier la somme (un peu du genre 1+2+3+...+n=n(n+1)/2), c'est peine perdue, il n'y en a pas.

Il y a juste le fait que cette série a une limite qui est donnée par GaBuZoMeu.