Sur-famille d'un vecteur qui n'appartient pas à SEV

[dengnarienfaitdemal]

Bonjour,

Dans un exercice, j'ai montré que le vecteur n'appartient pas à l'ensemble des solutions du système et j'ai donné une base à cette ensemble. La famille qui est composée des vecteurs de et du vecteur n'est donc pas liée (ni libre) puisque , non ?

[GaBuZoMeu]

Bonjour,

Posons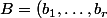 . Tu peux démontrer que est une famille libre. Tu sais comment procéder.

[dengnarienfaitdemal]

Faut-il démontrer que avec l'algorithme du pivot ou y a-t-il une méthode rapide, vu le contexte ? J'ai pensé qu'il y a une propriété à évoquer (que j'ai oublié) puisqu'on a montré que .

[GaBuZoMeu]

C'est un résultat général : si est une famille libre et ( n'est pas combinaison linéaire de ), alors la famille est libre. Tu peux le démontrer sans peine en revenant à la définition de famille libre.

[dengnarienfaitdemal]

D'accord, je vois le raisonnement, merci.