Bonsoir je rencontre des difficultés face au deux questions de l'exercice suivant pouvez vous m'éclairez sur le raisonnement merci d'avance
n est un nombre entier naturel non nul et a1, a2, …, an sont n nombres d’un intervalle I.
On note Pn la propriété f((a1+a2+...+an)/n) < (f(a1)+f(a2)+...+f(an))/n
1. a. Démontrer que, si f est une fonction convexe sur un intervalle I, alors pour tous nombres a, b, c et d de I : f((a+b+c+d)/4) <( f(a)+f(b)+f(c)+f(d))/4
Autrement dit, si P2 est vraie, alors P4 est vraie aussi.
b. En utilisant le même raisonnement, démontrer que si Pn est vraie alors P2n est vraie aussi.
comme indication nous avons: utiliser l'inégalité de convéxité f((x+y)/2) <( f(x)+f(y))/2
pour x et y bien choisis.
Convexité
10 messages
- Page 1 sur 1
Re: convexité
Bonjour,
Il n'y a que le dernier terme qui est divisé par n ? Quelles sont les priorités des opérations ?
Il n'y a que le dernier terme qui est divisé par n ? Quelles sont les priorités des opérations ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: convexité
bonjour non tout les termes sont divisé par n, j'ai oublié de mettre les parenthèse
, on a : f((a1+a2+...+an)/n) < (f(a1)+f(a2)+...+f(an))/n et montrer que : f((a+b+c+d)/4) <( f(a)+f(b)+f(c)+f(d))/4
je pense qu'il faut utiliser l'inégalité des fonction convexe qui est f((x+y)/2))<(f(x)+f(y))/2, mais le dénominateur me pose problème comment on passe de 2 à 4?
, on a : f((a1+a2+...+an)/n) < (f(a1)+f(a2)+...+f(an))/n et montrer que : f((a+b+c+d)/4) <( f(a)+f(b)+f(c)+f(d))/4
je pense qu'il faut utiliser l'inégalité des fonction convexe qui est f((x+y)/2))<(f(x)+f(y))/2, mais le dénominateur me pose problème comment on passe de 2 à 4?
Re: convexité
Peut-on écrire ceci ?
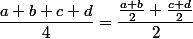
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: convexité
Si, du coup d'après la formule f((x+y)/2))<(f(x)+f(y))/2 avec x= a+b et y= c+d
on pourra a déduire que f( ( (a+b)/2 + ( c+d)/2 ) /2 ) < ( f((a+b)/2) + f((c+d)/2)) /2
de plus on sait que f( (a+b) /2)) < ( f(a)+f(b) )/2 de même pour c+d
on obtient au final 1/2( f( (a+b+c+d)/2) )< 1/2( (f(a)+f(b))/2 + (f(c)+f(d))/2 )
puis on distribue le 1/2 fin d'obtenir 4 au niveau du dénominateur
est-ce juste?
on pourra a déduire que f( ( (a+b)/2 + ( c+d)/2 ) /2 ) < ( f((a+b)/2) + f((c+d)/2)) /2
de plus on sait que f( (a+b) /2)) < ( f(a)+f(b) )/2 de même pour c+d
on obtient au final 1/2( f( (a+b+c+d)/2) )< 1/2( (f(a)+f(b))/2 + (f(c)+f(d))/2 )
puis on distribue le 1/2 fin d'obtenir 4 au niveau du dénominateur
est-ce juste?
Re: convexité
Oui c'est cela.
Il n'y a plus qu'à dérouler la "récurrence" (qui n'est pas vraiment une récurrence, car on ne passe pas de n à n+1...)
Il n'y a plus qu'à dérouler la "récurrence" (qui n'est pas vraiment une récurrence, car on ne passe pas de n à n+1...)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: convexité
d'accord merci.
du coup il faudra partir de la formule suivante f((a1+a2+...+an)/n) < (f(a1)+f(a2)+...+f(an))/n
et multiplier par 1/n se qui nous donnera f((a1+a2+...+a2n)/2n) < (f(a1)+f(a2)+...+f(a2n))/2n ?
du coup il faudra partir de la formule suivante f((a1+a2+...+an)/n) < (f(a1)+f(a2)+...+f(an))/n
et multiplier par 1/n se qui nous donnera f((a1+a2+...+a2n)/2n) < (f(a1)+f(a2)+...+f(a2n))/2n ?
Re: convexité
Euh non. Relisez bien ce que l'énoncé vous demande.
Et si vous ne "voyez pas bien", faites-le pas à pas : vous avez déjà le passage de 2 à 4, passez donc de 4 à 8 comme on l'a fait pour 2 à 4.
Et si vous ne "voyez pas bien", faites-le pas à pas : vous avez déjà le passage de 2 à 4, passez donc de 4 à 8 comme on l'a fait pour 2 à 4.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: convexité
du coup on pose (a1+...+an+...+a2n)/2 = ((a1+...+an)/2 + ( an+1+...+a2n)/2 ) /n
donc f( ( (a1+...+an)/2 + ( an+1+...+a2n)/2 ) /n ) < ( f((a1+...+an)/2) + f((an+1+...+a2n)/2)) /n
et on a f( (a1+...+an) /2)) < ( f(a1)+...+f(an) )/2 de même pour an+1+...+a2n
alors 1/n( f( (a1+...+an+...+a2n)/2) )< 1/n( (f(a1)+...+f(an))/2 + (f(an+1)+...+f(a2n))/2 )
pour finir on distribue le 1/n pour obtenir 2n au niveau du dénominateur.
c'est juste ?
donc f( ( (a1+...+an)/2 + ( an+1+...+a2n)/2 ) /n ) < ( f((a1+...+an)/2) + f((an+1+...+a2n)/2)) /n
et on a f( (a1+...+an) /2)) < ( f(a1)+...+f(an) )/2 de même pour an+1+...+a2n
alors 1/n( f( (a1+...+an+...+a2n)/2) )< 1/n( (f(a1)+...+f(an))/2 + (f(an+1)+...+f(a2n))/2 )
pour finir on distribue le 1/n pour obtenir 2n au niveau du dénominateur.
c'est juste ?
Re: convexité
Oui !
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
