THEOREME DE GAUSS et BEZOUT

[thibpln]

Bonjour a tous, je suis nouveau dans ce forum et je souhaiterai avoir de l'aide pour un exercice de maths expertes en option de Term.

l'exercice est posé sous forme de probleme.

a et b designent deux nombres entiers naturels premiers entre eux. on dispose d'un nombre non limite de pieces de a euros et un nombre non limite de piece de b euros.
Quelle est la plus grande somme que l'on ne peut pas payer avec ces pieces?

ca fait un bout de temps que je reflechis, je fais des test mais rien n'aboutit. C'est dans le chapitre du theoreme de bezout et de gauss mais je n'arrive pas a faire le lien.
Pour moi, on peux additionner a et b jusqu'a l'infini, cette question est bizarre.

Merci d'avance pour votre temps et pour votre aide.

a toute

[Rdvn]

Bonjour,
Il faut comprendre l'énoncé comme ceci :
on doit payer une somme n (entier, supérieur ou égal à 1) avec des pièces de a ou de b,
sans retour d'appoint.
Autrement dit, existe-t-il des entiers positifs x et y tels que xa + yb = n ?
A titre d'échauffement je vous propose de commencer par traiter un exemple :
a=5 et b=2 , qui sont bien premiers entre eux,
paramètre n (entier, supérieur ou égal à 1)
On cherche si il existe des entiers x e y positifs tels que 5x + 2y = n
On a l'égalité de Bezout-Bachet , ici évidente :
5 - 2*2 = 1
et donc 5n - 2*2n =n
Cela devrait commencer à vous dire quelque chose...
A vous : proposez un essai

PS au passage, cet exemple soulignera une difficulté à résoudre le cas général avec a et b ,

[GaBuZoMeu]

Bonjour,

thibpln s'est-il évaporé ?

Pour guider le travail, quelques jalons :

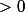Soient et des entiers premiers entre eux. Soit un entier .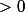
1) Montrer qu'il existe un unique couple d'entiers tels que 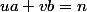et .
2) Montrer que l'on peut payer € en pièces de € et € si et seulement si l'entier de l'unique couple du 1) est positif ou nul.

[Rdvn]

Bonjour,
De ce que j'en sais, thibpin s'est évaporé...
J'attendais avant d'aller plus loin qu'il traite au moins mon exemple, avec 2 et 5,
pour pouvoir "rebondir" sur le cas général...aucun retour à cette heure

[GaBuZoMeu]

Je ne suis pas sûr que, pour ce problème, traiter l'exemple de 2 et 5 apporte beaucoup de pistes pour aborder le cas général. C'est pour cela que j'ai donné les indications ci-dessus.

[catamat]

Bonjour,

Merci d'avoir fait vivre ce post malgré la disparition de son créateur.

Le sujet m'intéresse et je ne connais pas la théorie le concernant donc je me contente d'utiliser les aides données.

On a donc a et b des entiers premiers entre eux et un entier n strictement positif.

D'après le théorème de Bezout il existe un couple d'entiers relatifs (s,t) tel que
as + bt = 1
donc on a asn + btn = n
ou au + bv = n (E1) en posant u=sn et v=tn,
(u,v) est aussi un couple d'entiers relatifs

Supposons que l'on ait un autre couple d'entiers relatifs (u',v') tels que au' + bv'=n (E2)

(E1)-(E2) donne a(u-u')=b(v'-v)

D'après le th de Gauss a et b étant premiers entre eux, a divise v'-v, donc ak=v'-v avec k dans Z.

On en conclut que u-u'=bk, donc finalement u'=u-bk et v'=v+ak.

La réciproque est immédiate donc tous les couples d'entiers relatifs (u',v') tels que n=au'+bv' sont de la forme
u'=u-bk, v'=v+ak, où (u,v) est une solution particulière et k est élément de Z.

On remarque que les v' sont congrus entre eux modulo a, ils font partie de la classe de v dans Z/aZ.

Or dans cette classe il y a un seul élément compris entre 0 et a-1

D'où la conclusion

[GaBuZoMeu]

Ça, c'était le point 1.
Ensuite ?

[Rdvn]

Bonsoir à tous ,

@GaBuZoMeu
En fait, en proposant un exemple numérique, je voulais surtout m'assurer que les « bases »
étaient là : connaissance et compréhension des théorèmes classiques, techniques de calcul.
Je pensais aussi me servir de cet exemple comme introduction au problème, sous entendu
mais non posé : désignons par E l'ensemble des entiers n tels que la somme n ne peut pas
être payée (déjà : remarquer que E est non vide) montrer que E est majoré, ce qui est difficile
pour un élève en Terminale .
Il ne fait pas de doute pour moi que votre présentation , ci dessus, aurait été un énoncé
beaucoup plus intéressant pour ce problème.
@catamat
C'est ce que j’espérais de thibpin, en plus facile puisque sur un exemple numérique
(sauf la fin de votre écrit, que je n'avais pas demandé)

[catamat]

Bon le point 2 selon moi :

Dans un sens c'est simple, étudions la réciproque.
On supposons que l'on peut former l'entier n en ajoutant des monnaies de valeur a ou b.
Donc on a : i et j entier positifs tels que n = ia + jb

Faisons la division euclidienne de j par a, on a
j=aq + r avec 0<=q et 0<= r < a, comme r est entier 0 <= r <= a-1.

En reportant dans ia + jb, on obtient :
n = ia + (aq + r)b
donc n = (i+qb)a + rb
en posant u=i+qb et v = r on obtient la conclusion car i+qb est positif et r compris entre 0 et a-1.

[GaBuZoMeu]

Bien, étapes 1) et 2) franchies. Et maintenant, la conclusion ? Quelle est la plus grande somme en € qu'on ne peut pas payer avec des pièces de a et b € ?

[catamat]

Oui là ça doit demander un peu d'astuce...

Pour le moment je vois que ua=n-bv donc u a le signe de n-bv

On sait que v<=a-1 donc -bv >= b-ab
Si n >= ab, on en déduit que n-bv >= b >0
Donc u est positif. Tout nombre supérieur à ab peut s'écrire comme somme de pièces de valeur a ou b.

Mais bon même si c'est une avancée cela ne répond pas à la question.

J'ai fait quelques essais avec un tableur, par ex pour a=17 et b=11 j'obtiens 159 comme plus grande somme impossible à atteindre...

Je vais continuer à chercher...

[catamat]

Bon, j'émet une conjecture, après quelques essais sur tableur, ce plus grand nombre serait ab-a-b.

On peut le vérifier pour 5 et 2,

5*2-5-2=3, c'est en effet le plus grand nombre impossible à atteindre.

Bon reste à la démontrer...

[GaBuZoMeu]

Les étapes 1) et 2) ont permis de cerner les n qui conviennent, et aussi par conséquent ceux qui ne conviennent pas (ceux pour lesquels on ne peut pas payer n € en pièces de a et b €). Ce sont les n qui peuvent s'écrire sous la forme ....
Une fois les points de suspension remplis, pas difficile de trouver le plus grand de ces n.

[catamat]

les n que l'on ne peut atteindre sont ceux qui s'écrivent au+bv avec u<0 et v compris entre 0 et a-1.

Donc pour maximiser la valeur de n il faut prendre u et v les plus grands possibles.

La plus grande valeur de u est -1 et la plus grande valeur de v est a-1 donc le plus grand n que l'on ne peut atteindre est -a+(a-1)b soit ab-a-b.

Ouf... merci beaucoup pour les aides précieuses.

[GaBuZoMeu]

Avec plaisir.

[lyceen95]

Pour ceux qui voudraient donner une suite à cet exercice ( 3 types de pièces différents, k types de pièces différents), cet exercice est connu sous le nom de Nombre de Frobenius.

[catamat]

Merci beaucoup j'allais justement poser cette question !