Les nombres complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Bob1sérieux
- Membre Relatif
- Messages: 102
- Enregistré le: 05 Avr 2020, 14:24
-
 par Bob1sérieux » 27 Fév 2021, 19:59
par Bob1sérieux » 27 Fév 2021, 19:59
Bonjour à tous,
Est-ce que vous pourriez m'aider pour un exercice s'il vous plait.
Question 1: Démontrer que pour tout réel a et b :
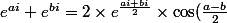)
Question 2: En déduire que
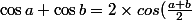 \times cos (\frac {a-b}{2}))
Merci d'avance pour votre aide
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 27 Fév 2021, 20:07
par hdci » 27 Fév 2021, 20:07
Bonjour,
Pour la question 1, il suffit simplement d'écrire le cosinus à l'aide des formules d'Euler (exponentielle complexe) et de développer pour vérifier qu'on retrouver bien la somme des deux exponentielles (autrement dit : partir de la fin plutôt que du début pour arriver au début par égalités successives).
Pour la question 2 : il suffit d'écrire les complexes sous forme algébrique et de dire que s'il y a égalité alors les parties réelles sont égales.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
Bob1sérieux
- Membre Relatif
- Messages: 102
- Enregistré le: 05 Avr 2020, 14:24
-
 par Bob1sérieux » 27 Fév 2021, 20:36
par Bob1sérieux » 27 Fév 2021, 20:36
Bonjour,
Merci pour votre réponse,
J'ai trouvé pour la question 1 mais je n'ai pas compris comment écrire les complexes sous forme algébrique pour la question 2. La formule ne contient que des cos donc le nombre est réel ?
Merci d'avance,
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 27 Fév 2021, 20:47
par hdci » 27 Fév 2021, 20:47
Si vous avez deux complexe z=a+ib et z'=a'+ib', alors z=z' implique a=a', mais cela ne veut pas dire que z est réel.
De quel complexe le réel cos(a)+cos(b) est-il la partie réelle ? (je parle bien sûr d'un complexe qui se trouve dans l'énoncé, il n'y a pas besoin de l'inventer, même s'il y a une infinité de complexes ayant cette partie réelle)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
Bob1sérieux
- Membre Relatif
- Messages: 102
- Enregistré le: 05 Avr 2020, 14:24
-
 par Bob1sérieux » 27 Fév 2021, 21:49
par Bob1sérieux » 27 Fév 2021, 21:49
Merci beaucoup j'ai trouvé
Bonne soirée !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités