Fonction et trigonométrie
14 messages
- Page 1 sur 1
Fonction et trigonométrie
Bonjour,
Je dois résoudre le problème suivant : « Soit les fonctions f et g définies sur [−π π; ] par
f(x)= 4sin^2(x) et g(x ) = 2x. Quelles sont les positions relatives des courbes
représentatives ?
Pour se faire j'ai posé h(x)= f(x)-g(x)=4sin^2(x)-2x
et je cherche ensuite quand h(x)=0 soit 4sin^2(x)-2x =0
Par contre je n'arrive pas à résoudre cette équation (sauf pour x=0). J'ai tenté de passer par le calcul de delta mais je n'obtiens pas les bons résultats
Si quelqu'un peut m'orienter ?
Je dois résoudre le problème suivant : « Soit les fonctions f et g définies sur [−π π; ] par
f(x)= 4sin^2(x) et g(x ) = 2x. Quelles sont les positions relatives des courbes
représentatives ?
Pour se faire j'ai posé h(x)= f(x)-g(x)=4sin^2(x)-2x
et je cherche ensuite quand h(x)=0 soit 4sin^2(x)-2x =0
Par contre je n'arrive pas à résoudre cette équation (sauf pour x=0). J'ai tenté de passer par le calcul de delta mais je n'obtiens pas les bons résultats
Si quelqu'un peut m'orienter ?
Re: Fonction et trigonométrie
Bonjour,
Il ne s'agit pas de déterminer si h(x)=0, mais de considérer le signe de h(x).
Il y a un intervalle sur lequel le résultat est immédiat (car on aura la somme de deux termes positifs)
Sur l'autre intervalle, l'étude des variations de h peut être utile.
Il ne s'agit pas de déterminer si h(x)=0, mais de considérer le signe de h(x).
Il y a un intervalle sur lequel le résultat est immédiat (car on aura la somme de deux termes positifs)
Sur l'autre intervalle, l'étude des variations de h peut être utile.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Fonction et trigonométrie
Merci pour ce retour
Par contre comment je détermine les points d'intersections qui amènent à un changement de signe ?
Par contre comment je détermine les points d'intersections qui amènent à un changement de signe ?
Re: Fonction et trigonométrie
Bonjour,
h(x)= f(x)-g(x)=4sin^2(x)-2x
Il faut étudier les variations de h(x) sur [-Pi ; Pi]
Avec 0 <= sin²(x) <= 1 , on sait directement que :
h(x) > 0 sur [-Pi ; 0[
et que
h(x) < 0 sur ]2 ; Pi]
Donc il suffit d'étudier les variations de h(x) sur [0 ; 2]
Ceci en étudiant le signe de h'(x) = ...
Tu trouveras ainsi les valeurs de x pour lesquels on a un minimum de h(x) et un maximum de h(x)
En calculant les valeurs de h(x) pour ces valeurs de x (celles pour le min et pour le max), tu trouveras le signe des ces extrema.
Et tu en déduiras les intervalles pour lesquels h(x) s'annule.
Les valeurs des passages par 0 de h(x) pourront alors être trouvées par approximations successives en se limitant à des intervalles où h est monotone (en s'aidant du tableau de variations de h)
...

h(x)= f(x)-g(x)=4sin^2(x)-2x
Il faut étudier les variations de h(x) sur [-Pi ; Pi]
Avec 0 <= sin²(x) <= 1 , on sait directement que :
h(x) > 0 sur [-Pi ; 0[
et que
h(x) < 0 sur ]2 ; Pi]
Donc il suffit d'étudier les variations de h(x) sur [0 ; 2]
Ceci en étudiant le signe de h'(x) = ...
Tu trouveras ainsi les valeurs de x pour lesquels on a un minimum de h(x) et un maximum de h(x)
En calculant les valeurs de h(x) pour ces valeurs de x (celles pour le min et pour le max), tu trouveras le signe des ces extrema.
Et tu en déduiras les intervalles pour lesquels h(x) s'annule.
Les valeurs des passages par 0 de h(x) pourront alors être trouvées par approximations successives en se limitant à des intervalles où h est monotone (en s'aidant du tableau de variations de h)
...
Re: Fonction et trigonométrie
Je dois avoir un problème sur le calcul de la dérivée car pour les extremum je ne retombe pas sur les ordonnées d'intersection de f(x) et g(x)
h(x)=4sin²(x)-2x et donc pour moi h(x)'=8sin(x)cos(x)-2
h(x)=4sin²(x)-2x et donc pour moi h(x)'=8sin(x)cos(x)-2
Re: Fonction et trigonométrie
Je cherche à trouver les ordonnées qui vont me permettre de définir les intervalles de mon tableau de variation
Re: Fonction et trigonométrie
Ton problème, c'est de trouver les  dans
dans 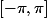 qui vérifient
qui vérifient \cos(x)-2=0) ? La présence de
? La présence de \cos(x)) , ça ne te fait pas penser à une formule trigonométrique ?
, ça ne te fait pas penser à une formule trigonométrique ?
Re: Fonction et trigonométrie
Je viens de revoir mon cours et je n'ai rien trouvé. J'ai aussi regardé sur le net et pas plus. Si tu peux m'aiguiller un peu plus ?
Re: Fonction et trigonométrie
Hum, pas sûr qu'au lycée on ait vu les formules trigo autre que celles avec plus ou moins pi, plus ou moins pi sur deux (elles ne sont pas au programme de la terminale spé).
Par contre on peut s'en tirer (c'est un peu plus calculatoire) en posant X=cos²(x) puis sin²(x)=1-X et résoudre une inéquation en X du second degré : il s'agit de résoudre sur [0,pi]
\cos(x)-2\geq 0)
On peut remarquer que sur [pi/2,pi] c'est jamais vrai car le cosinus est négatif.
Donc on étudie sur [0,pi/2] et cela donne
\cos(x)\geq 1)
qu'on peut élever au carré
\cos^2(x)\geq 1)
Soit avec X=cos²(x)

Et on trouve les intervalles pour X pour lesquels c'est vrai, d'où pour cos²(x).
Sinon, la formule trigo dont parle GaBuMoZeu est
=2\sin(x)\cos(x))
Par contre on peut s'en tirer (c'est un peu plus calculatoire) en posant X=cos²(x) puis sin²(x)=1-X et résoudre une inéquation en X du second degré : il s'agit de résoudre sur [0,pi]
On peut remarquer que sur [pi/2,pi] c'est jamais vrai car le cosinus est négatif.
Donc on étudie sur [0,pi/2] et cela donne
qu'on peut élever au carré
Soit avec X=cos²(x)
Et on trouve les intervalles pour X pour lesquels c'est vrai, d'où pour cos²(x).
Sinon, la formule trigo dont parle GaBuMoZeu est
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Fonction et trigonométrie
Désolé mais je sèche
Pour faire le tableau de variation il me faut les abscisses des intersections en f(x) et g(x)
Et pour les trouver, résoudre h(x)=0 avec h(x)=f(x)-g(x)=4sin²(x)-2x
Graphiquement je trouve x=0, x=0,555 et x=1,849 (c'est dommage je ne peux ajouter le graphique)
Mais je n'arrive vraiment pas à trouver ces points par calcul. Si vous avez la solution ?
Pour faire le tableau de variation il me faut les abscisses des intersections en f(x) et g(x)
Et pour les trouver, résoudre h(x)=0 avec h(x)=f(x)-g(x)=4sin²(x)-2x
Graphiquement je trouve x=0, x=0,555 et x=1,849 (c'est dommage je ne peux ajouter le graphique)
Mais je n'arrive vraiment pas à trouver ces points par calcul. Si vous avez la solution ?
Re: Fonction et trigonométrie
Mais peut-être ne faut-il pas calculer ces abscisses, mais simplement dire qu'elles existent et en donner un encadrement ?
L'étude de la fonction dérivée donne le sens de variation de h.
On va donc trouver, par exemple, que h est croissante entre une abscisse x1 et une abscisse x2 (que là part contre on sait déterminer, cf. ce qui a été écrit précédemment, soit avec la formule trigo, soit avec le polynôme en X=cos²(x)), et que h(x1)<0 et h(x2)>0, cela indique clairement grâce à un certain théorème qui parle d'intermédiaire qu'il existe un réel x0 tel que h(x0)=0, et on sait qu'après x0 h est positive et avant h est négative.
Et cela donne la position relative des courbes, on sait juste que x0 existe, on l'a encadré, et on peut éventuellement l'encadrer par dichotomie de façon plus précise mais il n'y aura pas de "solution-formule exacte".
L'étude de la fonction dérivée donne le sens de variation de h.
On va donc trouver, par exemple, que h est croissante entre une abscisse x1 et une abscisse x2 (que là part contre on sait déterminer, cf. ce qui a été écrit précédemment, soit avec la formule trigo, soit avec le polynôme en X=cos²(x)), et que h(x1)<0 et h(x2)>0, cela indique clairement grâce à un certain théorème qui parle d'intermédiaire qu'il existe un réel x0 tel que h(x0)=0, et on sait qu'après x0 h est positive et avant h est négative.
Et cela donne la position relative des courbes, on sait juste que x0 existe, on l'a encadré, et on peut éventuellement l'encadrer par dichotomie de façon plus précise mais il n'y aura pas de "solution-formule exacte".
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Fonction et trigonométrie
Je vais faire comme tu me dis
Toujours un grand merci aux contributeurs
Toujours un grand merci aux contributeurs
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
