Je vois que
Domaine d'une limite dans une racine
15 messages
- Page 1 sur 1
Domaine d'une limite dans une racine
Bonjour,
Je vois que}=\sqrt[n]{ \lim_{x\to a} f(x)}) mais il faut que
mais il faut que >0) pour
pour  pair. Ce que je ne comprends pas c'est pourquoi cela doit être plus grand que 0. Le domaine d'une racine c'est
pair. Ce que je ne comprends pas c'est pourquoi cela doit être plus grand que 0. Le domaine d'une racine c'est 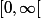 et non
et non 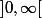
Je vois que
Re: Domaine d'une limite dans une racine
fibonacci a écrit:bonsoir
exact n dit être de la forme 2k.
Merci pour ton aide très pertinente à me question
Re: Domaine d'une limite dans une racine
GaBuZoMeu a écrit:Merci de l'attention portée à l'aide que je t'ai fournie.
Je n'ai pas encore compris le message que tu as voulu me dire.
Je suis d'accord que l'on peut avoir
Re: Domaine d'une limite dans une racine
Une des réponse que je vois c'est que 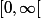 est un intervalle et sur un intervalle, la continuité d'une limite est définie si elle est continue dans l'intervalle
est un intervalle et sur un intervalle, la continuité d'une limite est définie si elle est continue dans l'intervalle 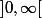 et que
et que =f(a))
Re: Domaine d'une limite dans une racine
C'était pourtant simple : si <0) pour tout
pour tout  et si
et si  est pair, alors le terme de gauche de l'égalité n'est pas défini, ce qui est assez gênant.
est pair, alors le terme de gauche de l'égalité n'est pas défini, ce qui est assez gênant.
C'est pour éviter ça que l'on suppose>0) . Ceci assure que l'on a
. Ceci assure que l'on a  >0) au voisinage de
au voisinage de  , et alors
, et alors }) a bien un sens, même si
a bien un sens, même si  est pair.
est pair.
C'est pour éviter ça que l'on suppose
Re: Domaine d'une limite dans une racine
Supposons f(x) = -x pour x dans ]-oo ; 0[
a = 0 et n = 2
lim(x-->a) f(x) = lim(x-->0) (-x) = 0
et donc} = \sqrt{0} = 0)
Alors que}) n'existe pas.
n'existe pas.

Edit:
Pas vu le message précédent avant d'envoyer le mien.
a = 0 et n = 2
lim(x-->a) f(x) = lim(x-->0) (-x) = 0
et donc
Alors que
Edit:
Pas vu le message précédent avant d'envoyer le mien.
Re: Domaine d'une limite dans une racine
Et tu n'as pas vu non plus que si
alors>0) pour tout
pour tout  du domaine de définition de
du domaine de définition de  .
. 
Black Jack a écrit:f(x) = -x pour x dans ]-oo ; 0[
alors
Re: Domaine d'une limite dans une racine
Pourquoi on aurait pas pu dire \ge 0) ?
?
Ce qui me dérange le plus c'est l'exclusion du 0, car est définie
est définie
Ce qui me dérange le plus c'est l'exclusion du 0, car
Re: Domaine d'une limite dans une racine
Bonjour,
Si on sait que f est positive au voisinage de a, alors vous avez raison l'inégalité est large.
Mais si on ne sait pas si f est positive au voisinage de a on ne sait rien dire.
Par exemple, la fonction) est de limite nulle en 0. Mais au voisinage de 0 elle prend des valeurs strictement positives et strictement négatives, il n'y a pas de voisinage pour lequel elle reste strictement positive. Par suite la racine n-ème (où n est pair) n'existe pas sur un intervalle autour de 0, alors qu'elle existe en 0 et en une infinité de nombres autour de 0.
est de limite nulle en 0. Mais au voisinage de 0 elle prend des valeurs strictement positives et strictement négatives, il n'y a pas de voisinage pour lequel elle reste strictement positive. Par suite la racine n-ème (où n est pair) n'existe pas sur un intervalle autour de 0, alors qu'elle existe en 0 et en une infinité de nombres autour de 0.
Si on sait que f est positive au voisinage de a, alors vous avez raison l'inégalité est large.
Mais si on ne sait pas si f est positive au voisinage de a on ne sait rien dire.
Par exemple, la fonction
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Domaine d'une limite dans une racine
Spyrakos, pourrais-tu faire un petit effort pour lire et comprendre ce qu'on te dit ?
On te serine sur tous les tons que si=0) , alors on n'est pas assuré que
, alors on n'est pas assuré que \geq 0) au voisinage de
au voisinage de  et donc on n'est pas assuré de pouvoir donner un sens à
et donc on n'est pas assuré de pouvoir donner un sens à }) au voisinage de
au voisinage de  quand
quand  est pair.
est pair.
On te serine sur tous les tons que si
Re: Domaine d'une limite dans une racine
GaBuZoMeu a écrit:Spyrakos, pourrais-tu faire un petit effort pour lire et comprendre ce qu'on te dit ?
On te serine sur tous les tons que si
Ce n'est pas de la mauvaise volonté. Je comprends que quelque chose m'échappe dans votre raisonnement et je cherche simplement des exemples pour mieux visualiser votre façon de raisonner
Re: Domaine d'une limite dans une racine
On t'a déjà donné des exemples !
Prends définie par
définie par  = -|x|) .
.
Tu as bien}=0) , mais quel sens donnerais-tu à
, mais quel sens donnerais-tu à }) ?
?
Prends
Tu as bien
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
