Congruence et classe d'équivalence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
eltheola
- Messages: 7
- Enregistré le: 18 Fév 2021, 11:38
-
 par eltheola » 18 Fév 2021, 17:43
par eltheola » 18 Fév 2021, 17:43

Bonjour, quelqu'un pourrait m'aider à comprendre/résoudre cet exercice s'il vous plaît ? Merci.
Montrer que 13 divise 2^70 + 3^70 et que 11 divise 2^129 + 118.
-
janor
- Membre Naturel
- Messages: 26
- Enregistré le: 12 Fév 2021, 11:47
-
 par janor » 18 Fév 2021, 18:04
par janor » 18 Fév 2021, 18:04
Bonjour, pour montrer que a divise b, il faut montrer que b ≡ 0 [a] car cela signifie que b = k.a avec k un réel.
-
eltheola
- Messages: 7
- Enregistré le: 18 Fév 2021, 11:38
-
 par eltheola » 18 Fév 2021, 18:15
par eltheola » 18 Fév 2021, 18:15
Merci du conseil mais dans le corrigé on nous dit que c'est égal à classe de 4^35+ classe de 9^35 ce que je ne comprends pas
-
mathelot
 par mathelot » 18 Fév 2021, 18:22
par mathelot » 18 Fév 2021, 18:22
c'est une formule de puissances qui est valable dans N , sans utiliser de congruence:
a et n entiers relatifs:
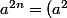^n)
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 18 Fév 2021, 18:26
par hdci » 18 Fév 2021, 18:26
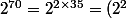^{35}=4^{35})
On fait de même avec
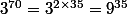
Ensuite on remarque que

puisque
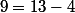
.
Et les congruences se conservent avec les puissances, c-à-d.
^{35}[13])
D'où
^{35}[13])
Et c'est terminé pour le premier.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités

