Fonction et représentation graphique

[Baptistercl80]

https://imageshack.com/i/poS2QVr7j

Bonjour quelqu’un pourrais m’aider pour l’exercie 1 a 7 sur la photo via le lien merci

[hdci]

Bonjour,

Une grande partie des réponses se trouvent dans votre cours de maths, celui que vous avez pris en note avec le professeur.
Par exemple : dans l'exercice 1, on vous demande de lire un graphique et en cours le prof vous a forcément donné les indications, l'axe des abscisses, l'axe des ordonnées, ce qu'est une image, un antécédent, et comment la courbe représentative est construite.

Avant de poster l'ensemble des exercices, vous devez faire l'effort (je sais, ce n'est pas facile) de travailler avec votre cours, et s'il y a des choses de votre cours que vous ne comprenez pas, on pourra vous les expliquer. Mais juste lister les exercices comme ça, sans aucune autre information, ce n'est pas efficace ni une bonne méthode de travail.

[Baptistercl80]

Désolé mais si je pose ça c’est que malheureusement je n’est pas eu de cours car la prof s’en fou complètement et nous laisse sans cours

[mathelot]

bonsoir,

exercice 1

est la courbe représentative de f dans un repère
On a l'équivalence
M est un point quelconque du plan de coordonnées (x;y)



Application:



question 1.b

f(-1)=0 se traduit par "0 est l'image de -1 par f"

exercice 2
Graphiquement, les points et appartiennent à la courbe de f:
On en déduit
f(3)=20 et f(4)=50
d'où

exercice 3
x est un antécédent de y par f .

remarque: si , x a une unique image notée f(x). Par contre x est un antécédent de y et y peut avoir plusieurs antécédent. Par exemple, si f est une fonction paire, on a
y=f(x)=f(-x) . si x est non nul, y admet au moins deux antécédents: x et -x.

[mathelot]

Les courbes sont à peine visibles sur la photo. Peux tu poster des photos, exercice par exercice ?

[Baptistercl80]

Oui bien sûr
Exercice 1
https://imageshack.com/i/pmQMC5Ouj
Exercice 2 et 3
https://imageshack.com/i/poX8BQgGj
Exercice 4 et 5
https://imageshack.com/i/pmvn7cbpj
Exercice 6 et 7
https://imageshack.com/i/pmGGgv0ej
Exercice 8 et 9
https://imageshack.com/i/pmS3rbv6j
Exercice 10
https://imageshack.com/i/poJouZW0j

[mathelot]

voici quelques remarques:
exercice 1
d'où f(2)=3 , 2 est un antécédent de 3 par f.
donc 1 et -1 sont des antécédents de zéro par f.
exercice 2
donc f(...)=... (compléter les petits points)
exercice 3
) sont des points de la courbe
exercice 4.c
appartient à la courbe
exercice 5.b
appartient à la courbe
exercice 6
sur l'axe des ordonnées, l'unité est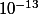 , 10 unités valent
exercice 7
Le point ) appartient à la courbe
exercice 8
courbe des amplitudes, la fonction représentée est de période 2,i.e, pour tout t réel,
on appelle ce genre de courbe une "sinusoïde"