Bonjour à tous s'il vous plaît j'essaie de déterminer le Domaine de définition de la fonction suivante
F(x)= sin x / ( cos x + sinx) besoin d'indications
Études des fonctions
12 messages
- Page 1 sur 1
Re: Études des fonctions
Bonjour,
Le domaine de définition sera tel que le dénominateur ne s'annule pas.
Le dénominateur est nul pour+\sin(x)=0) , soit
, soit =-\sin(x)) .
.
Or on sait que+\sin^2(x)=1)
Sachant que=-\sin(x)) , on en déduit aisément les valeurs possibles pour le cosinus qui annulent le dénominateur, ce qui donne un ensemble de réels x susceptibles d'annuler le dénominateur. Si on se retreint à la mesure principale (entre -pi et pi), cela fait exactement 4 valeurs possibles pour x.
, on en déduit aisément les valeurs possibles pour le cosinus qui annulent le dénominateur, ce qui donne un ensemble de réels x susceptibles d'annuler le dénominateur. Si on se retreint à la mesure principale (entre -pi et pi), cela fait exactement 4 valeurs possibles pour x.
Il n'y a plus qu'à identifier ceux parmi ces quatre qui ont un sinus opposé au cosinus (il y en a deux). On en déduit le domaine de définition restreint à la mesure principale, puis par périodicité le domaine de définition dans IR.
Le domaine de définition sera tel que le dénominateur ne s'annule pas.
Le dénominateur est nul pour
Or on sait que
Sachant que
Il n'y a plus qu'à identifier ceux parmi ces quatre qui ont un sinus opposé au cosinus (il y en a deux). On en déduit le domaine de définition restreint à la mesure principale, puis par périodicité le domaine de définition dans IR.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Études des fonctions
En remplaçant les expressions cos ^2 x + sin ^2 =1 dans l'expression sinx+cosx=0 on obtient 2cos^2 x = 1
=> cos x = √2/2 => cos x = cos π/4
La résolution donne x= π/4 + 2kπ ou x =-π/4 +2kπ
Est ce exact ?
=> cos x = √2/2 => cos x = cos π/4
La résolution donne x= π/4 + 2kπ ou x =-π/4 +2kπ
Est ce exact ?
Re: Études des fonctions
Oui, et non.
=1) est correct, et cela implique bien
est correct, et cela implique bien =\dfrac{1}{2})
Mais cela n'implique pas=\dfrac{\sqrt{2}}{2}) ; il manque quelque chose.
; il manque quelque chose.
Comment résolvez-vous l'équation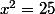 ? Il n'y a pas qu'une seule solution...
? Il n'y a pas qu'une seule solution...
Mais cela n'implique pas
Comment résolvez-vous l'équation
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Études des fonctions
Variante qui évite les solutions parasites dues à l'élévation au carré :
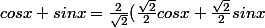= \frac{2}{\sqrt2} cos(x-\frac{\pi}{4}))
Les zéros de cette expression sont donc donnés par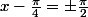
soit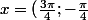)
On aurait pu voir directement sur le cercle trigonométrique les positions où le sinus et le cosinus ont une valeur opposée ...
Les zéros de cette expression sont donc donnés par
soit
On aurait pu voir directement sur le cercle trigonométrique les positions où le sinus et le cosinus ont une valeur opposée ...
Re: Études des fonctions
Effectivement,
mais au niveau lycée, les formules trigonométriques ne sont pas au programme (sauf les plus ou moins pi et plus ou moins pi/2).
mais au niveau lycée, les formules trigonométriques ne sont pas au programme (sauf les plus ou moins pi et plus ou moins pi/2).
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Études des fonctions
J'ai finalement trouvé 3π/4 qui correspond à la seule valeur qui annule l'expression et dont les valeurs sont opposées
Donc mon domaine de définition est R-{3π/4}
Donc mon domaine de définition est R-{3π/4}
Re: Études des fonctions
Non ce n'est pas la seule solution.
Quelles sont les 4 valeurs possibles pour que le cosinus soit égal à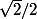 ? Vous en avez donné deux au début, vous en donnez une troisième, quelle est la quatrième ?
? Vous en avez donné deux au début, vous en donnez une troisième, quelle est la quatrième ?
Pour chacune de ces valeurs, quel est le sinus ?
Quelles sont les 4 valeurs possibles pour que le cosinus soit égal à
Pour chacune de ces valeurs, quel est le sinus ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Études des fonctions
J'ai procédé à la résolution de cet équation
Cos x = √2/2 ou cos x = -√2/2.
Je parviens alors à
X=π/4.+ 2kπ
X=-π/4 + 2kπ
X=3π/4+2kπ
X=-3π/4+2kπ
Cos x = √2/2 ou cos x = -√2/2.
Je parviens alors à
X=π/4.+ 2kπ
X=-π/4 + 2kπ
X=3π/4+2kπ
X=-3π/4+2kπ
Re: Études des fonctions
Je déduis à l'aide du tableau trigonométrique que le seul x qui vérifie l'équation cosx=-sinx est 3π/4
C'est correct ?
C'est correct ?
Re: Études des fonctions
Demgo a écrit:Je déduis à l'aide du tableau trigonométrique que le seul x qui vérifie l'équation cosx=-sinx est 3π/4
C'est correct ?
non, hélas.
d'où
d'où deux points sur le cercle trigo d'abscisses curvilignes
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
