Si je ne me trompe pas
Difference entre cosec et sin^-1
4 messages
- Page 1 sur 1
Difference entre cosec et sin^-1
Bonjour,
Si je ne me trompe pas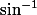 est la fonction inverse de
est la fonction inverse de 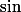 càd
càd 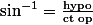 . Mais quelle est la difference entre
. Mais quelle est la difference entre 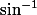 et
et  . J'ai l'impression que c'est pareil
. J'ai l'impression que c'est pareil
Si je ne me trompe pas
Re: Difference entre cosec et sin^-1
Attention à la notation )
Dans la majorité des applications,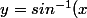) est écrit pour
est écrit pour 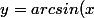) , c'est à dire que la valeur renvoyée y est celle comprise dans [-Pi/2 ; Pi/2] qui a x pour sinus.
, c'est à dire que la valeur renvoyée y est celle comprise dans [-Pi/2 ; Pi/2] qui a x pour sinus.
A ne pas confondre avec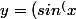\ )^{-1}) ... qui elle est équivalente à
... qui elle est équivalente à } = csc(x))
********
La notation) est d'origine anglo-saxonne, je pense, la notation européenne étant
est d'origine anglo-saxonne, je pense, la notation européenne étant ) .
.
Malheureusement, la notation anglosaxonne est de plus en plus employée même en Europe (ne serait-ce que via les calculettes, qui utilisent cette notation).
... Et cela engendre bien des incompréhensions (comme celle exprimée ici dans ta question)
********
On a évidemment des problèmes similaires avec)) et
et )) utilisées pour
utilisées pour ) et
et )
*******
Le risque de confusion est d'autant plus grand qu'on a pris l'habitude d'écrire par exemple : sin²(x) au lieu de (sin(x))² et que dès lors, si on étend cette "habitude" avec un exposant "-1" on ne peut plus distinguer 1/sin(x) de arcsin(x) si on écrit)
Comme on ne peut pas empêcher ces notations (que je qualifierai pour ma part d'idiotes) largement répandues, on ne peut le faire qu'en réfléchissant à la nature du problème qui utilisent ces notations.
Avec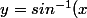) :
:
a) Si y doit être un angle (ou un arc), alors c'est que) doit être compris comme
doit être compris comme )
b) si y est sans unité, alors c'est que) doit être compris comme
doit être compris comme })
Exemples simples :
Dans l'expression : Pi/2 +) = 1,2
= 1,2
) doit avoir la même unité que Pi/2 ... donc être en radian, donc être un angle (ou un arc)
doit avoir la même unité que Pi/2 ... donc être en radian, donc être un angle (ou un arc)
---> ici) doit être compris comme arcsin(x)
doit être compris comme arcsin(x)
Dans l'expression : tan(x) +) = 2,75
= 2,75
) doit avoir la même unité que tan(x), donc pas d'unité ...
doit avoir la même unité que tan(x), donc pas d'unité ...
---> ici) doit être compris comme 1/sin(x)
doit être compris comme 1/sin(x)
*******
Pour éviter la confusion, il serait mieux d'éviter les notations comme) pour 1/sin(x)
pour 1/sin(x)
En espérant ne pas t'avoir brouillé d'avantage.

Dans la majorité des applications,
A ne pas confondre avec
********
La notation
Malheureusement, la notation anglosaxonne est de plus en plus employée même en Europe (ne serait-ce que via les calculettes, qui utilisent cette notation).
... Et cela engendre bien des incompréhensions (comme celle exprimée ici dans ta question)
********
On a évidemment des problèmes similaires avec
*******
Le risque de confusion est d'autant plus grand qu'on a pris l'habitude d'écrire par exemple : sin²(x) au lieu de (sin(x))² et que dès lors, si on étend cette "habitude" avec un exposant "-1" on ne peut plus distinguer 1/sin(x) de arcsin(x) si on écrit
Comme on ne peut pas empêcher ces notations (que je qualifierai pour ma part d'idiotes) largement répandues, on ne peut le faire qu'en réfléchissant à la nature du problème qui utilisent ces notations.
Avec
a) Si y doit être un angle (ou un arc), alors c'est que
b) si y est sans unité, alors c'est que
Exemples simples :
Dans l'expression : Pi/2 +
---> ici
Dans l'expression : tan(x) +
---> ici
*******
Pour éviter la confusion, il serait mieux d'éviter les notations comme
En espérant ne pas t'avoir brouillé d'avantage.
Re: Difference entre cosec et sin^-1
En d'autres mots...
On parle de l'inverse d'un nombre , et par ailleurs de l'inverse d'une fonction.
Et je vais tout de suite corriger : on parle de l'inverse d'un nombre, et par ailleurs de la réciproque d'une fonction. (par abus de langage, on utilise aussi le mot fonction inverse... mais pour clarifier, je préfère le mot fonction réciproque).
Ces 2 concepts nombre inverse et fonction réciproque sont assez différents, mais le piège, c'est qu'on retrouve dans les 2 cas l'exposant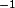 et aussi on retrouve le mot inverse.
et aussi on retrouve le mot inverse.
L'inverse d'un nombre d'abord : L'inverse de 3, c'est 1/3 ; l'inverse de , c'est
, c'est 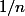 , qu'on note également
, qu'on note également 
La fonction réciproque de sin, c'est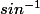 qu'on note souvent
qu'on note souvent 
Si = y) , alors
, alors  = x) , ou encore
, ou encore  = x)
) : l'exposant
: l'exposant 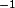 s'applique à la fonction
s'applique à la fonction 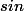 : c'est la fonction réciproque de la fonction
: c'est la fonction réciproque de la fonction 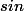 , c'est
, c'est )
)^{-1}) : l'exposant
: l'exposant 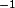 s'applique au nombre
s'applique au nombre ) : c'est le nombre inverse du nombre
: c'est le nombre inverse du nombre ) , c'est le nombre
, c'est le nombre 
Si on retrouve la même notation (exposant -1) pour ces 2 concepts différents, ce n'est pas pour piéger les élèves... il y a une certaine logique à utiliser la même notation. Une logique incontestable.
On parle de l'inverse d'un nombre , et par ailleurs de l'inverse d'une fonction.
Et je vais tout de suite corriger : on parle de l'inverse d'un nombre, et par ailleurs de la réciproque d'une fonction. (par abus de langage, on utilise aussi le mot fonction inverse... mais pour clarifier, je préfère le mot fonction réciproque).
Ces 2 concepts nombre inverse et fonction réciproque sont assez différents, mais le piège, c'est qu'on retrouve dans les 2 cas l'exposant
L'inverse d'un nombre d'abord : L'inverse de 3, c'est 1/3 ; l'inverse de
La fonction réciproque de sin, c'est
Si
Si on retrouve la même notation (exposant -1) pour ces 2 concepts différents, ce n'est pas pour piéger les élèves... il y a une certaine logique à utiliser la même notation. Une logique incontestable.
Re: Difference entre cosec et sin^-1
Bonjour,
Tout le truc c'est que ce n'est que dans le supérieur qu'on peut vraiment comprendre pourquoi cet "exposant -1" pour une réciproque... Il faut avoir abordé des notions de loi de composition interne, d'élément neutre, ede symétrique...
Pour simplifier : l'inverse d'un nombre x, c'est le nombre y tel que xy=1, où 1 est l'élément neutre de la multiplication (quand on multiplie par 1 on "reste sur le même nombre" en quelque sorte). On a ici une "opération dans l'ensemble des nombres", la multiplication.
Quand on se place non plus dans un ensemble de nombres, mais dans un ensemble de fonctions, on peut (sous réserve de quelques conditions que j'omettrais ici) définir une opération : la "composition". On note cela "rond", avec deux fonctions f et g, on définit la fonction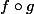 comme étant la fonction qui à x associe f(g(x)) (on "enchaîne" les fonctions).
comme étant la fonction qui à x associe f(g(x)) (on "enchaîne" les fonctions).
Et là on se rend compte que la fonction qui à x associe x est un élément neutre pour cette opération : en effet, si on appelle Id cette fonction, alors et
et 
Du coup, s'il existe une fonction g telle que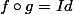 , alors g est "l'inverse" de f au regard de cette opération "rond". D'où la notation
, alors g est "l'inverse" de f au regard de cette opération "rond". D'où la notation 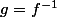 , par "analogie" avec l'inverse d'un nombre au regard de la multiplication.
, par "analogie" avec l'inverse d'un nombre au regard de la multiplication.
Tout le truc c'est que ce n'est que dans le supérieur qu'on peut vraiment comprendre pourquoi cet "exposant -1" pour une réciproque... Il faut avoir abordé des notions de loi de composition interne, d'élément neutre, ede symétrique...
Pour simplifier : l'inverse d'un nombre x, c'est le nombre y tel que xy=1, où 1 est l'élément neutre de la multiplication (quand on multiplie par 1 on "reste sur le même nombre" en quelque sorte). On a ici une "opération dans l'ensemble des nombres", la multiplication.
Quand on se place non plus dans un ensemble de nombres, mais dans un ensemble de fonctions, on peut (sous réserve de quelques conditions que j'omettrais ici) définir une opération : la "composition". On note cela "rond", avec deux fonctions f et g, on définit la fonction
Et là on se rend compte que la fonction qui à x associe x est un élément neutre pour cette opération : en effet, si on appelle Id cette fonction, alors
Du coup, s'il existe une fonction g telle que
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
