Sous-grouoes discrets de R^n

[0577215]

Bonjour,
Dans le cadre d'une démonstration, j'ai supposé qu'un sous-groupes de R^n engendré de partie génératrice finie est discret. Ça m'a permis d'aboutir mais je n'arrive pas à démontrer proprement ce point. Est ce que cela serait faux (je n'ai pas réussi à exhiber de contre-exemple) et si c'est vrai pourriez vous m'aidez à démontrer ça proprement ?

Merci d'avance

[0577215]

Il suffit de montrer que 0 est un point isolé donc que deux éléments du sous-groupe ne peuvent être arbitrairement proche mais je n'y arrive. Peut être que c'est faux si vous avez un contre-exemple je suis preneur.

[0577215]

Finalement j'ai le sentiment que ça ne marche pas avec juste l'hypothèse une partie génératrice finie, je précise l'hypothèse une partie génératrice finie d'éléments de Q^n

[GaBuZoMeu]

Que penses-tu du sous groupe de engendré par et ?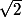

Je vois que tu t'es aperçu du problème. Si tu pars d'un nombre fini de générateurs dans , c'est comme si tu considérais un sous-groupe de 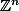(à homothétie près).

[0577215]

Ah bah oui bien sûr. Bon je montrais que mon sous-groupe H engendré par une partie finie de Q^n était isomorphe à un sous groupe de Z^n grâce à ma supposition qu'il était discret mais du coup c'est encore plus direct.
Merci à vous, bonne journée