Bonsoir,
Je rencontre beaucoup de difficultés pour un exercice non corrigé, pourriez vous s'il vous plait m'aider.
(Espaces L^p ).
Soit (X, A(ronde) , µ) un espace mesuré, p ∈ [1, ∞[ et A ∈ A(ronde). On pose F = {f ∈ L^p (X, A(ronde), µ) : f = 0 sur A µ-pp}. Montrer que F est fermé dans L^p (X, A(ronde), µ)
Merci d'avance.
Aide exercice espace Lp
2 messages
- Page 1 sur 1
Re: Aide exercice espace Lp
Bonjour,
Voila une piste :
Suppose qu'il existe une suite_{n\in\mathbb{N}}) de
de  convergent vers une fonction
convergent vers une fonction  dans
dans 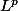 . Pour montrer que
. Pour montrer que  est dans F, il suffit alors de montrer que
est dans F, il suffit alors de montrer que 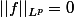 .
.
Voila une piste :
Suppose qu'il existe une suite
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
