Déterminant

[jeje56]

Bonjour à tous,
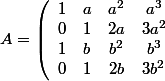Il s'agit d'abord de calculer le déterminant de la matrice . Je trouve .
Il s'agit ensuite de montrer que quelles que soient les valeurs de f(a), f(b), f'(a), f'(b) données, il existe un unique polynôme de degré inférieur ou égal à 3 vérifiant . Je ne vois pas...
Merci de votre aide précieuse.

[GaBuZoMeu]

Bonsoir,

La matrice que tu as écrite n'est pas la bonne : il y a un qui devrait être un 1. Vérifie.
Comment je le sais ? Parce que c'est la matrice du système en les coefficients indéterminés de qui exprime que ont des valeurs prescrites. Ça devrait te mettre sur la voie.

[jeje56]

Merci Gabu,
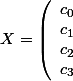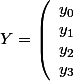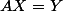
En posant et , résoudre revient à déterminer les coefficients du polynôme f vérifiant , , et ...
Reste à vérifier que est non nul pour justifier l'unicité de f... Est-ce le cas ?
Merci !

[GaBuZoMeu]

Pas besoin de ça pour montrer l'unicité de f.
Il suffit de voir que si h est un polynôme de degré au plus 3 tel que h(a)=h'(a)=h(b)=h'(b)=0; alors h est le polynôme nul.

[jeje56]

Pas besoin de ça pour montrer l'unicité de f.
Il suffit de voir que si h est un polynôme de degré au plus 3 tel que h(a)=h'(a)=h(b)=h'(b)=0; alors h est le polynôme nul.

Donc AX=0 équivaut à X=0 ce qui prouve que A est inversible et que f est unique...

[GaBuZoMeu]

Vois-tu bien ce qu'il suffit de voir ?

[jeje56]

Je pense... Ma dernière phrase le dit non ?

[GaBuZoMeu]

Eh ben non, ta dernière phrase ne le dit pas.
Relis-toi.

Elle dit "Donc ... ", en embrayant sur mon affirmation, mais rien ne dit que tu sais prouver mon affirmation.
Si tu le sais, tant mieux. Mais je n'ai pas la preuve que tu le sais.
Peux-tu m'expliquer comment tu démontres mon affirmation ?

[mathelot]

bonjour,

[jeje56]

bonjour,

Exact ! Je viens de refaire les calculs. Merci Mathelot !