Bonjour,
spyrakos a écrit:2. L'écrivant sous la forme

et mn=ac et m+n=b
Euh non, c'est plutôt (attention au signe et il faut aussi remplacer le coefficient constant)
x+mn)
Cela provient directement du développement de
(x-n))
Le truc dans la méthode 2, c'est qu'il faut connaître m et n. Et connaître m et n, c'est factoriser le polynôme (résoudre
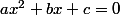
) car m et n sont les deux racines du polynômes, si elles existent.
Donc si vous ne connaissez pas m et n, et que vous ne les devinez pas, la méthode 2 est inutile car impossible à faire sans repasser par la méthode 1.
Exemple ;

: ici, on peut "deviner" que 1+2=3 et 1x2=2 d'où m=1, n=2.
Mais si on ne le devine pas, vous les trouvez en calculant avec le discriminant.
Il y a enfin une autre méthode, celle de la factorisation par une "racine évidente".
Par exemple, dan

, on "voit" que x=1 est une racine (le calcul est immédiat). Donc on aura
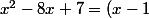(x-n))
et le n se déduit du coefficient constant (n=7 en l'occurence)
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.

