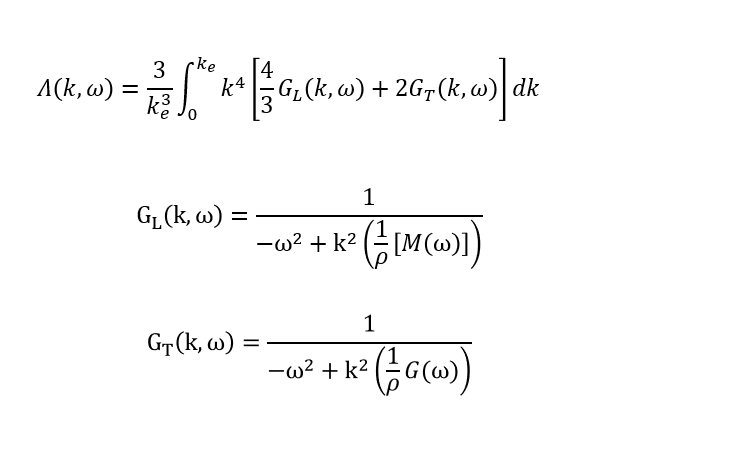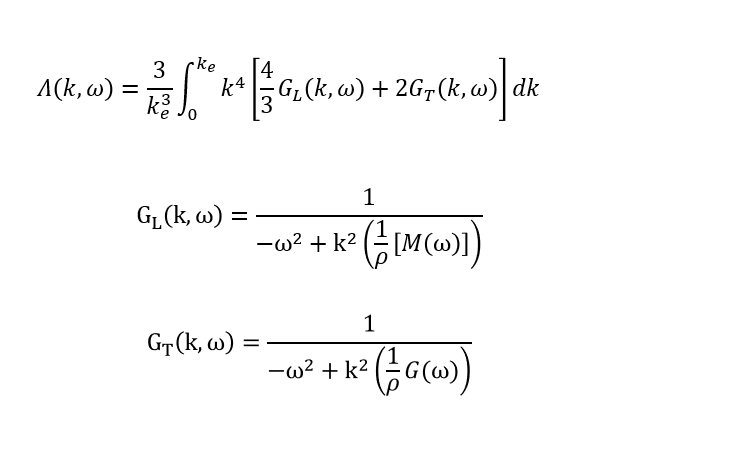Je souhaite intégrer cette fonction, quelqu'un pourrait m'aider ?
Merci par avance.
Intégration
5 messages
- Page 1 sur 1
Intégration
par BosonPeak » 28 Jan 2021, 18:21
Bonsoir,
Je souhaite intégrer cette fonction, quelqu'un pourrait m'aider ?
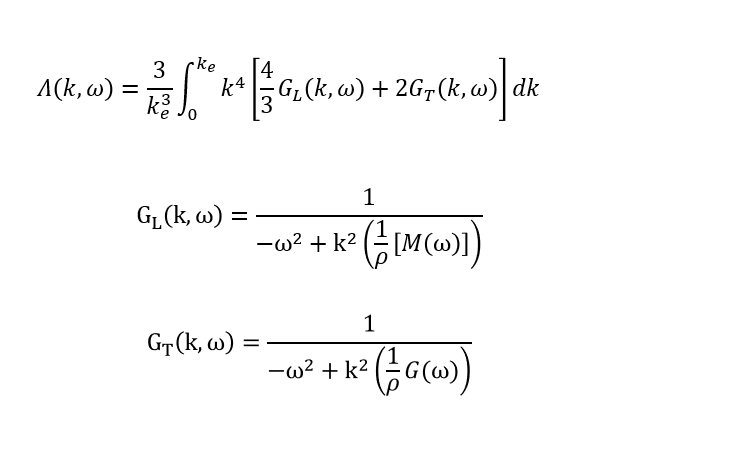
Merci par avance.
Je souhaite intégrer cette fonction, quelqu'un pourrait m'aider ?
Merci par avance.
Re: Intégration
par mathelot » 28 Jan 2021, 18:57
bonsoir,
pour faire avancer les choses (*) on peut chercher à calculer
(*) le schmilblick
pour faire avancer les choses (*) on peut chercher à calculer
(*) le schmilblick
Re: Intégration
par mathelot » 28 Jan 2021, 22:03
On suppose ])
et 
strictement positifs.
on coupe l'intégrale en deux , en utilisant la linéarité:
on pose:
:=\dfrac{4}{k_e^3} \int_{0}^{k_e} \, k^4 G_{L} (k,\omega) dk)
:=\dfrac{6}{k_e^3} \int_{0}^{k_e} \, k^4 G_{T} (k,\omega) dk)
=\dfrac{4}{k_e^3} \int_0^{k_e} \, \dfrac{x^4}{\frac{[M(\omega)]}{\rho} (x^2-(\omega\sqrt{\frac{\rho}{[M(\omega)]}})^2)} dx)
on utilise I(a) (c.f (*))
=\dfrac{4\rho}{k_e^3[M(\omega)]} \left[ \, \dfrac{k_e^3}{3}+\dfrac{\omega^2 \rho k_e}{[M(\omega)]} +\dfrac{1}{2} \dfrac{\omega^3 \rho \sqrt{\rho} } {[M(\omega)] \sqrt{[M(\omega)]}}Ln \left|\dfrac{k_e-\omega\sqrt{\dfrac{\rho}{[M(\omega)]}}} {k_e+\omega\sqrt{\dfrac{\rho}{[M(\omega)]}}}\right| \right])
=\dfrac{4\rho}{3[M(\omega)]} +\dfrac{4\omega^2 \rho^2}{k_e^2[M(\omega)]^2} +\dfrac{2\omega^3 \rho^2 \sqrt{\rho} } {k_e^3[M(\omega)]^2 \sqrt{[M(\omega)]}}Ln \left|\dfrac{k_e-\omega\sqrt{\dfrac{\rho}{[M(\omega)]}}} {k_e+\omega\sqrt{\dfrac{\rho}{[M(\omega)]}}}\right| \right])
où |.| désigne la valeur absolue.
on coupe l'intégrale en deux , en utilisant la linéarité:
on pose:
on utilise I(a) (c.f (*))
où |.| désigne la valeur absolue.
Modifié en dernier par mathelot le 29 Jan 2021, 17:58, modifié 6 fois.
Re: Intégration
par mathelot » 28 Jan 2021, 22:34
on a coupé l'intégrale en deux , on traite )
:
=\dfrac{6}{k_e^3} \int_0^{k_e} \, \dfrac{x^4}{\dfrac{G(\omega)}{\rho} (x^2-(\omega\sqrt{\frac{\rho}{G(\omega)}})^2)} dx)
C'est la même intégrale que
mais avec un facteur 6 et )
à la place de
=\dfrac{2\rho}{G(\omega)} +\dfrac{6\omega^2 \rho^2}{k_e^2 G(\omega)^2} +\dfrac{3\omega^3 \rho^2 \sqrt{\rho} } {k_e^3 G(\omega)^2 \sqrt{G(\omega)}}Ln \left|\dfrac{k_e-\omega\sqrt{\dfrac{\rho}{G(\omega)}}} {k_e+\omega\sqrt{\dfrac{\rho}{G(\omega)}}}\right| \right])
C'est la même intégrale que
à la place de
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :