Continuité: Fonction Auxiliaire

[Bob1sérieux]

Bonjour à tous,
J'espère que vous allez bien,
Je bloque à la dernière question (B. 3.),
Pourriez-vous m'aider ?

Énoncé: https://www.casimages.com/i/210127075328711094.png.html

Je vous remercie par avance,
Bien à vous,

[hdci]

Bonjour,

Pour commencer il y a une erreur dans l'énoncé, la fonction f devrait être donnée par



Avec cette précision, et l'information , on sait déterminer les variations de f et en particulier l'abscisse de son maximum local sur 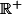: pourquoi ?

Une fois déterminée cette abscisse, il s'agit de calculer son image : je vous laisse faire ce calcul, dans l'attente j'appelle cette image (vous remplacerez bêta par ce que vous aurez trouvé).

Alors vous calculez (mise au même dénominateur, factorisation etc.) pour faire apparaître une expression que vous saurez être nulle grâce à la partie A : ce qui prouve l'égalité

(car si vous montrez alors vous avez montré

[Bob1sérieux]

Bonjour, Oui j'ai effectivement oublié de signaler l'erreur,
L'abscisse de maximum demandé est α.
Don le maximum de f sur l'intervalle demandé est f(α),
Donc il faut montrer que f(α)=α^3 / (α+2) ?
Soit β = f(α) ?

Bien à vous

[hdci]

Oui c'est bien cela, mais plutôt que de démontrer l'égalité, calculez la différence (cela revient au même mais cela évite de terminer par "équivaut à 0=0")