je n'arrive pas à comprendre cette égalité, quelqu'un peut m'éclairer?
Opérations sur des sommes
5 messages
- Page 1 sur 1
opérations sur des sommes
Bonjour à tous,
je n'arrive pas à comprendre cette égalité, quelqu'un peut m'éclairer?
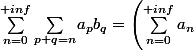\left( \sum_{n=0}^{+inf}b_{n}\right))
je n'arrive pas à comprendre cette égalité, quelqu'un peut m'éclairer?
Re: opérations sur des sommes
Bonjour,
La somme de gauche c'est
+(a_1b_0+a_0b_1)+(a_2b_0+a_1b_1+a_0b_2)+\cdots)
Elle s'appelle "produit de Cauchy"
Le produit des deux sommes de droite c'est
(b_0+b_1+b_2+\cdots))
Si les deux séries de terme (a_n) et (b_n) sont absolument convergente, il y a alors égalité. Cela résulte, en gros, du fait que dans une famille sommable, l'ordre des termes n'a pas d'importance et quand on développe la somme de droite, on retrouve les termes de la somme de gauche, et chaque terme de la somme de gauche est égal à un seul des termes développés de la somme de droite. S'il n'y a pas absolue convergence, on ne peut rien dire (l'absolue convergence est une condition suffisante pour avoir ce résultat)
La somme de gauche c'est
Elle s'appelle "produit de Cauchy"
Le produit des deux sommes de droite c'est
Si les deux séries de terme (a_n) et (b_n) sont absolument convergente, il y a alors égalité. Cela résulte, en gros, du fait que dans une famille sommable, l'ordre des termes n'a pas d'importance et quand on développe la somme de droite, on retrouve les termes de la somme de gauche, et chaque terme de la somme de gauche est égal à un seul des termes développés de la somme de droite. S'il n'y a pas absolue convergence, on ne peut rien dire (l'absolue convergence est une condition suffisante pour avoir ce résultat)
Modifié en dernier par hdci le 27 Déc 2020, 12:20, modifié 1 fois.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: opérations sur des sommes
mathelot a écrit:
En supposant les réelset
positifs, on a donc:
pour p,q,n,N entiers naturels:
Grâce au théorème des gendarmes, le produit de Cauchy tend vers le produit des deux séries
quand N tend vers l'infini:
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

