Décomposition en élément simple
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 23 Déc 2020, 14:31
par elvis77 » 23 Déc 2020, 14:31
Bonjour,
J'ai un doute pour calculer les coefficients dans une DES, voici la fraction :
(1-x^2)(1-x^5)})
Je trouve :
(1-x^2)(1-x^5)}=\dfrac{1}{10(1-x)^3}+\dfrac{1}{4(1-x)^2}+\dfrac{13}{40(1-x)}+\dfrac{1}{8(x+1)}+\sum_{k=1}^4\dfrac{\lambda_k}{x-\omega_k})
avec
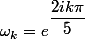
et ma question porte sur les

(je ne suis pas sûr, pour les autres coefficients, pas de soucis)
Je trouve :
})
Merci pour votre aide ou vérification, cordialement.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 23 Déc 2020, 17:08
par GaBuZoMeu » 23 Déc 2020, 17:08
Bonjour,
Je trouve l'opposé en évaluant
(1-x^2)})
en
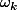
: l'un de nous deux s'est trompé de signe.
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 23 Déc 2020, 18:22
par elvis77 » 23 Déc 2020, 18:22
Merci de vous être penché sur mon calcul, c'est normal de trouver l'opposé, j'ai modifié quelque peu l'énoncé et oublié cette histoire de signe.
En tout cas, je suis soulagé que nous trouvions la même chose, en plus avec une forme plus élégante de votre part ce qui m'aidera pour la suite de mes calculs.
Un grand merci !
Cordialement.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 23 Déc 2020, 18:49
par GaBuZoMeu » 23 Déc 2020, 18:49
Avec plaisir.
Serais-tu en train de calculer le nombre de façons de payer n centimes en pièces de 1,2 et 5 centimes ?
Si oui, s'embêter avec les
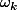
, c'est se compliquer beaucoup la vie.
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 23 Déc 2020, 19:02
par elvis77 » 23 Déc 2020, 19:02
Héhé, bien vu. Remarque, avec la tête de la fraction rationnelle, elle ne peut servir qu'à cela.
Dans le FGN Analyse 2, une application est proposée en faisant ensuite le DSE on obtient :
(n+2)}{20}+\dfrac{(-1)^n}{8}+\dfrac{\epsilon_n}{5})
avec

selon la congruence avec 5 donc je pensais utiliser les
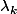
mais je bloque d'où ma question de départ : je voulais m'assurer que les
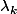
étaient juste.
Si vous avez une solution sans les
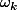
je suis preneur.
Merci,
Cordialement.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 23 Déc 2020, 22:50
par GaBuZoMeu » 23 Déc 2020, 22:50
Écrire la partie polaire relative aux pôles
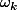
sous la forme

avec

polynôme de degré
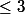
, et ensuite pour développer en série entière écrire ça sous la forme
P}{1-x^5})
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 24 Déc 2020, 11:32
par elvis77 » 24 Déc 2020, 11:32
Merci pour votre réponse mais je bloque sur le DSE, je suis "habitué" à faire des DSE sur les types de fonction bien connus après avoir faire une DES mais là je ne vois pas comment procéder ?
Cordialement.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 24 Déc 2020, 14:07
par GaBuZoMeu » 24 Déc 2020, 14:07
Tu as un problème avec le développement en série entière de quoi ?
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 24 Déc 2020, 18:37
par elvis77 » 24 Déc 2020, 18:37
Je n'arrive pas à faire le DSE de
P}{1-x^5})
car d'habitude je mets en élément simple pour pouvoir faire le DSE mais là je ne vois pas comment faire ? Merci pour votre aide.
Cordialement.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 24 Déc 2020, 19:06
par GaBuZoMeu » 24 Déc 2020, 19:06
Je parie que tu sais écrire le développement en série entière de

. Et après, multiplier cette série entière par le polynôme
P)
de degré
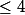
, ça vient tout seul. Non ?
Mais n'y passe pas le réveillon !
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 24 Déc 2020, 19:28
par elvis77 » 24 Déc 2020, 19:28
Merci pour la réponse.
J'obtiens :
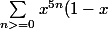P(x))
et si je développe en prenant
=ax^3+bx^2+cx+d)
j'ai :
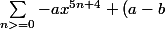x^{5n+3}+(b-c)x^{5n+2}+(c-d)x^{5n+1}+dx^{5n})
et ensuite je doit prendre le coefficient qui correspond à

mais je suis bloqué.
Peut-être qu'il vaut mieux exploiter cette écriture :
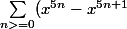P(x))
?
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 24 Déc 2020, 19:29
par elvis77 » 24 Déc 2020, 19:29
Cordialement.
PS : \seq ne semble pas fonctionner pour écrire "supérieur ou égal"
-
mathelot
 par mathelot » 24 Déc 2020, 19:32
par mathelot » 24 Déc 2020, 19:32
\geq
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 24 Déc 2020, 19:42
par GaBuZoMeu » 24 Déc 2020, 19:42
Il faut tout de même calculer le polynôme P (plusieurs manières de le faire).
Après, on aura une série entière avec des coefficients de

dépendant de

modulo 5.
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 24 Déc 2020, 22:38
par elvis77 » 24 Déc 2020, 22:38
Après de pénibles calculs, j'obtiens :
=\dfrac{1}{5}(X^3+2X^2+X+1))
puis le DSE :

mais je n'arrive pas "à voir et conclure modulo 5", je n'arrive pas à écrire quelque chose comme :

Cordialement.
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 25 Déc 2020, 19:30
par elvis77 » 25 Déc 2020, 19:30
J'ai une idée mais je n'arrive pas à la formaliser :
Faire un changement d'indice à l'aide de la partie entière de

.
Je sens bien que si n est congru à 3 ou 4 modulo 5 on obtient -1 puisque c'est le signe qu'il y a devant

et

. De même si n est congru à 0 ou 2 on obtient +1 et pour n congru à 1 on obtient 0 car il n'y a pas de terme en

mais je n'arrive pas à le formaliser.
Merci.
Cordialement.
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 25 Déc 2020, 20:49
par elvis77 » 25 Déc 2020, 20:49
Je pense avoir trouvé une explication satisfaisante.
Par exemple, on écrire :

Puis de comprendre qu'on partitionne n selon les différentes congruences modulo 5, on pourrait l'écrire de la façon suivante :
x^n+\sum_{n\equiv 3[5]}(-1)x^n+\sum_{n\equiv 2[5]}1.x^n+\sum_{n\equiv 1[5]}1.x^n+\sum_{n\equiv 0[5]}1.x^n)
Ainsi on obtient le coefficient devant

.
Merci pour votre aide.
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 25 Déc 2020, 20:56
par elvis77 » 25 Déc 2020, 20:56
Oups, pour l'avant-dernier il y a un facteur 0 devant...

-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Déc 2020, 11:20
par GaBuZoMeu » 26 Déc 2020, 11:20
La solution du paresseux : demander à un esclave numérique de faire le boulot (ici SageMath) :
- Code: Tout sélectionner
x=var('x')
F=1/(1-x)/(1-x^2)/(1-x^5)
DES=F.partial_fraction_decomposition()
print("Décomposition en éléments simples sur les rationnels :")
print(DES)
print("Numérateur du premier élément simple multiplié par 1-x :")
print((DES[0].numerator()*(1-x)).expand())
Décomposition en éléments simples sur les rationnels :
[1/5*(x^3 + 2*x^2 + x + 1)/(x^4 + x^3 + x^2 + x + 1), 1/8/(x + 1), -13/40/(x - 1), 1/4/(x - 1)^2, -1/10/(x - 1)^3]
Numérateur du premier élément simple multiplié par 1-x :
-x^4 - x^3 + x^2 + 1
-
elvis77
- Membre Relatif
- Messages: 156
- Enregistré le: 05 Fév 2008, 19:52
-
 par elvis77 » 26 Déc 2020, 13:16
par elvis77 » 26 Déc 2020, 13:16
C'est ce que j'avais fait en premier lieu avec Wolfram en ligne mais je voulais vérifier si le logiciel n'avait pas fait une erreur

C'est plutôt l'esclave qui demande au maître-numérique... A méditer !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
