Bonjour, je voulais juste savoir si ce qui suit est correct (si les équivalences sont bien des équivalences) :
(DB) ⃗∙(DC) ⃗ + (DC) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
<=>
(BD) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
<=>
‖(BD) ⃗ ‖ ≤ ‖(DC) ⃗ ‖
<=>
BD ≤ DC
Inéquation produit scalaire
9 messages
- Page 1 sur 1
Re: Inéquation produit scalaire
(Les points d'interrogations correspondent aux flèches des vecteurs)
Re: Inéquation produit scalaire
Bonsoir,
Je ne comprends pas ce passage
Le terme (DC) ⃗∙(DC) ⃗ se trouvant à droite ET à gauche, il ne peut pas simplement disparaître à gauche tout en restant à droite.
Je ne comprends pas ce passage
bapbap354 a écrit:(DB) ⃗∙(DC) ⃗ + (DC) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
<=>
(BD) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
Le terme (DC) ⃗∙(DC) ⃗ se trouvant à droite ET à gauche, il ne peut pas simplement disparaître à gauche tout en restant à droite.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Inéquation produit scalaire
Ce que je voulais dire, c'est que
Est faux en général !
Remplacez par des x et des y : vous avez écrit
 ;
;
Voyez-vous où est le problème ?
Voyez-vous un contre-exemple ?
bapbap354 a écrit:(DB) ⃗∙(DC) ⃗ + (DC) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
<=>
(BD) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
Est faux en général !
Remplacez par des x et des y : vous avez écrit
Voyez-vous où est le problème ?
Voyez-vous un contre-exemple ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Inéquation produit scalaire
Ducoup c'est mieux comma ça ?
(DB) ⃗∙(DC) ⃗ + (DC) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
<=>
(DB) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
Avec des x et des y ça donne:
x + y ≤ y <=> x ≤ y et là je ne vois pas de contre-exemple.
Si en fait je raconte toujours des bêtises, pouvez vous me dire si il est possible à partir de la première inéquation de démontrer que BD ≤ DC.
(DB) ⃗∙(DC) ⃗ + (DC) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
<=>
(DB) ⃗∙(DC) ⃗ ≤ (DC) ⃗∙(DC) ⃗
Avec des x et des y ça donne:
x + y ≤ y <=> x ≤ y et là je ne vois pas de contre-exemple.
Si en fait je raconte toujours des bêtises, pouvez vous me dire si il est possible à partir de la première inéquation de démontrer que BD ≤ DC.
Re: Inéquation produit scalaire
Vous avez

Si vous voulez avoir simplement x à gauche, vous devez retirer y.
Mais si vous retirez y d'un côté, vous devez retire y de l'autre côté également pour garantir l'équivalence. C'est la principe de la balance : si elle est déséquilibrée, et si vous retirez ou ajoutez un poidss d'un côté, vous devez retirer ou ajouter le même poids, sinon le déséquilbre n'est plus le même.
Ici, vous avez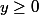 puisque c'est le carré de la norme du vecteur DC.
puisque c'est le carré de la norme du vecteur DC.
Donc on a , puisque
, puisque  et que
et que 
Mais vous n'avez pas l'équivalence. En effet, si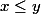 , alors on ne sait rien dire de
, alors on ne sait rien dire de 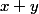 .
.
Contre-exemple : : on a bien
: on a bien  (donc
(donc 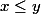 ) mais
) mais  qui est plus grand que
qui est plus grand que  .
.
La seule équivalence que vous pouvez utilisez est celle-ci

Si vous voulez avoir simplement x à gauche, vous devez retirer y.
Mais si vous retirez y d'un côté, vous devez retire y de l'autre côté également pour garantir l'équivalence. C'est la principe de la balance : si elle est déséquilibrée, et si vous retirez ou ajoutez un poidss d'un côté, vous devez retirer ou ajouter le même poids, sinon le déséquilbre n'est plus le même.
Ici, vous avez
Donc on a
Mais vous n'avez pas l'équivalence. En effet, si
Contre-exemple :
La seule équivalence que vous pouvez utilisez est celle-ci
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Inéquation produit scalaire
bapbap354 a écrit:Si en fait je raconte toujours des bêtises, pouvez vous me dire si il est possible à partir de la première inéquation de démontrer que BD ≤ DC.
La première équation vous dit par équivalence (en appliquant mon message précédent) que
Pourvez-vous trouver un contre-exemple qui fait que
(Ce n'est pas très long à trouver ; penser à une raison simple qui fait que le produit scalaire est négatif et trouvez un "très grand" vecteur
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: Inéquation produit scalaire
Le cosinus peut être négatif. Je pense être parti dans la mauvaise direction. Pour faire plus simple voilà le lien de l'énoncé : https://drive.google.com/file/d/1-yE-Y4 ... sp=sharing
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
