Equation différentielle
18 messages
- Page 1 sur 1
 Equation différentielle
Equation différentielle
Bonjour je n'arrive pas à résoudre l'équation différentielle suivante :
e^-xy' ÷ 2xe^-xy = 2x+1
Pourriez-vous m'aidez svp ?
e^-xy' ÷ 2xe^-xy = 2x+1
Pourriez-vous m'aidez svp ?
Re: Equation différentielle
Bonjour,
l'énoncé peut s'écrire, comme :
:
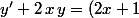\,e^x)
équation différentielle linéaire du 1er ordre , de forme classique
l'énoncé peut s'écrire, comme
équation différentielle linéaire du 1er ordre , de forme classique
Re: Equation différentielle
Oui c'est ce que j'ai fait.
Puis j'ai trouvé l'équation homogéne mais je n'arrive pas à trouver l'équation particuliére ?
Puis j'ai trouvé l'équation homogéne mais je n'arrive pas à trouver l'équation particuliére ?
Re: Equation différentielle
Alors je trouve yh(x)= Ce^(-x^2) avec C dans R.
Puis je pose C = B(x).
Et j'arrive à B(x)= intégrale de (2xe^(x+x^2)+e^(x+x^2).
Mais je n'arrive pas à calculer cette intégrale donc j'ai peut-être fait une erreur de calculs avant ?
Puis je pose C = B(x).
Et j'arrive à B(x)= intégrale de (2xe^(x+x^2)+e^(x+x^2).
Mais je n'arrive pas à calculer cette intégrale donc j'ai peut-être fait une erreur de calculs avant ?
Re: Equation différentielle
Oui j'ai obtenu cela mais ensuite il faut trouver C et je n'y arrive pas.
À partir de ca j'ai posé C'e^(-x^ )-2xCe^(-x^2) +Ce^(-x^2) = e^x(2x+1).
Mais après ???
À partir de ca j'ai posé C'e^(-x^ )-2xCe^(-x^2) +Ce^(-x^2) = e^x(2x+1).
Mais après ???
Re: Equation différentielle
MATHYS45560 a écrit:Oui j'ai obtenu cela mais ensuite il faut trouver C et je n'y arrive pas.
À partir de ca j'ai posé C'e^(-x^ )-2xCe^(-x^2) +Ce^(-x^2) = e^x(2x+1). c'est faux
Re: Equation différentielle
Oui donc ensuite :
C' = ((e^x)(2x+1))/ (e^(-x^2)) = (e^(x^2+x))(2x+1) = 2e^(x+x^2) + e^(x+x^2)
Donc ensuite on cherche C :
Intégrale de tout ça sauf que je n'arrice pas à le calculer.
???
C' = ((e^x)(2x+1))/ (e^(-x^2)) = (e^(x^2+x))(2x+1) = 2e^(x+x^2) + e^(x+x^2)
Donc ensuite on cherche C :
Intégrale de tout ça sauf que je n'arrice pas à le calculer.
???
Re: Equation différentielle
Oui j'arrive au même résultat que vous pour C'. Mais comment yrouver C à partir de ce résultat ?
Re: Equation différentielle
C'est bon j'ai trouvé la solution générale :
yg(x) =e^x + C e^(-x^2)
Merci beaucoup !
yg(x) =e^x + C e^(-x^2)
Merci beaucoup !
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
